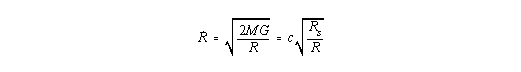
| zum nächsten Artikel | zum vorhergehenden Artikel | zurück zur Artikelauswahl | Kontakt | Englisch |
| Inhalt |
Zu einigen Problemen der modernen Kosmologie
IV. Ergänzungen
von St. Haase, Leipzig, BRD
Zusammenfassung:
Hier werden einige Ergänzungen zu den bereits erschienenen Teilen dieser Aufsatzreihe mitgeteilt. Insbesondere wird noch einmal auf den
Unterschied zwischen der in Teil I abgeleiteten Hubble-Relation und der in der Literatur auffindbaren Hubble-Beziehung eingegangen. - Die
Annahme, daß sich ruhemassebehaftete kosmische Objekte nicht schneller als mit Lichtgeschwindigkeit bewegen können, führt zu einer heute
maximal möglichen Expansionszeit für das Universum von texp = 7,37 x 109 Jahren. Hierdurch wird die beobachtbare Rotverschiebung auf zmax
= 1,25 begrenzt. Für die mittlere Rotverschiebung ergibt sich deshalb <z> = 0,418. Zum Expansionsbeginn war der Radius des Universums
gerade mit dem Schwarzschild-Radius RS = 1424 Mpc identisch. Die heutige Expansionsgeschwindigkeit des Universums beträgt 2/3 der
Lichtgeschwindigkeit. Die maximale Dichte des Universums betrug zu Beginn der Expansion mit rmax = 8,32 x 10-29 g cm-3 nur das 11,4-fache
der heute feststellbaren Dichte rA. - Für die Zurückblickzeit als Funktion der Rotverschiebung bzw. der scheinbaren Helligkeit werden einfache
Gleichungen angegeben.
Abstract:
Some supplementations to already published parts of this essay are given. In particular we again deal with differences between the Hubble relation derived in part I and the Hubble relationship which can be found in the literature. The assumption that cosmic objects with rest mass cannot move faster than at speed of light, gives a today's maximum possible expansion time of texp = 7.37 x 109 years for the universe. Hereby the observable red shift is limited to zmax = 1.25. Therefore the mean red shift is < z > = 0.418. At the beginning of the expansion the radius of the
universe was equal to the Schwarzschild radius RS = 1424 Mpc. The present velocity of expansion of the universe amounts to 2/3 of the speed of light. The maximum density of the universe rmax = 8.32 x 10-29 g cm-3 at the time of the beginning of the expansion was only 11,4 times the present ascertainable density rA. - Simple equations for the looking back time as function of the red shift and the apparent brightness, respectively, are given.
Key words: cosmology, Hubble relation, lock back time, red shift, Hubble time, expansion rate
1. Expansion des Universums und Hubble-Relation
In Teil I dieser Aufsatzreihe (St. Haase, 2000) wurde für die Beschreibung der Bewegung einer Beobachtergalaxie die Friedmann-Gleichung
| (I,10) | 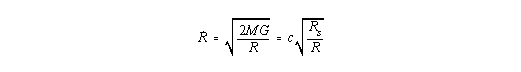
|
Die unbestimmte Integration von Gleichung (I,10) ergibt für das Weg-Zeit-Gesetz des Radius der Materiekugel
| (1) | 
|
| (2) | 
|
| (3) | 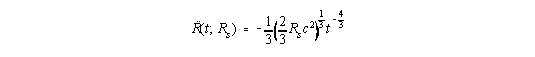
|
| (4) | 
|
| (5) | 
|
| (I,22) | 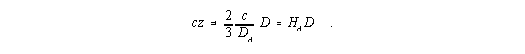
|
| (I,21) | 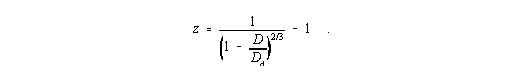
|
2. Expansionszeit, maximale Rotverschiebung und Expansionsgeschwindigkeit
Da auch im Rahmen der Kosmologie die Forderung der Nichtüberschreitbarkeit der Lichtgeschwindigkeit für ruhemassebehaftete Materie besteht, ergibt sich aus der Friedmann-Gleichung (I,10) die Bedingung, daß stets R ³ RS gelten muß. Dieser kleinstmögliche Radius der Materiekugel führt zu einem ganz konkreten Zeitpunkt für den Beginn der kosmologischen Expansion. Dieser hier als Schwarzschild-Zeit tS bezeichnete Zeitpunkt wird nach Gleichung (1) zu
| (6) | 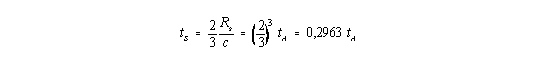
|
| (I,16) | 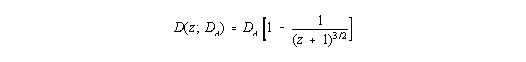
|
An dieser Stelle sei auf die Abb.3 von Teil II der vorliegenden Aufsatzreihe erinnert: Dort findet sich das Maximum für die mittlere Rotverschiebung bei <z> = 0,4192 für eine Grenzrotverschiebung von zmax = 1,3. Für zmax = 1,25 wird <z> = 0,418 gefunden. Die Differenz zwischen den beiden Rotverschiebungsgrenzwerten könnte ihre Ursache in der noch recht ungenauen Bestimmung des Hubble-Parameters haben. Wird aus theoretischer Sicht verlangt, daß die maximal meßbare Rotverschiebung genau zmax = 1,3 betragen sollte, ergibt sich ein heutiger Hubble-Parameter von H = 61,5 km s -1 Mpc -1 statt H = 62,34 km s-1 Mpc-1.
Auf Grund der Begrenzung der Geschwindigkeit der Kugeloberfläche auf die des Lichtes liegen alle theoretisch erwarteten Rotverschiebungswerte vor dem Maximum der Kurve von Abb. (II,3), wodurch die in dieser Abbildung vorhandene Zweideutigkeit für die mittlere Rotverschiebung ausgeschlossen wird.
Während die Expansion des Universums offenbar mit der Ausdehnungsgeschwindigkeit der kosmischen Materiekugel dR/dt = c begann (wobei der Radius des Universums gerade R = RS betrug), beträgt diese Geschwindigkeit gegenwärtig
| (7) | 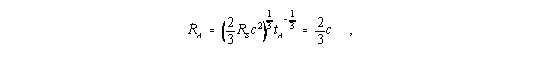
|
Die recht große Hubble-Zeit tH markiert die Tangente im Weg-Zeit-Gesetz zum heutigen Zeitpunkt: Wenn sich die Beobachtergalaxie schon immer mit der heutigen Geschwindigkeit bewegt hätte (d.h. nie schneller oder langsamer), gäbe es die Expansionsbewegung schon tH Jahre, allerdings nur, wenn auch R < RS zugelassen wäre.
Der maximale Lichtweg Dmax verkörpert gleichzeitig die maximale gravitative Einflußsphäre, d.h. Gebiete, die weiter voneinander entfernt sind, als es Dmax angibt, konnten sich bisher gravitativ nicht beeinflussen.
3. Größe und Dichte des Universums
Eine weitere interessante Beziehung ergibt sich aus der Gleichung (I,16b)
| (I,16b) | 
|
| (8) | 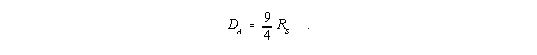
|
Weil die Masse des sichtbaren Teils vom Universum im Verlauf der Expansion konstant bleibt [vgl. mit Gleichung (I,15)], folgt für die Dichte dieser kugelförmig gedachten Materieverteilung der Zusammenhang
| (9) | 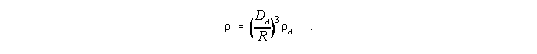
|
| (10) | 
|
Für den Lichtweg D = DA - RS (dies ist die von der Beobachtergalaxie bisher zurückgelegte Distanz) ist die Rotverschiebung nach Gleichung (I,16) gerade z = 0,7171. Diese Tatsache ermöglicht eine ebenso einfache wie interessante Erklärung für das Maximum in der Abb. (II,2): Die meisten kosmischen Objekte je Rotverschiebungsintervall sind genau für den Lichtweg (scheinbarer Abstand der beobachteten Galaxien) sichtbar, der der Ausdehnungsstrecke des Universums seit Beginn der Expansion entspricht. Zu dem zugehörigen Zeitpunkt waren die Galaxien am dichtesten beieinander! Galaxien mit einer heute größeren Rotverschiebung waren zum Emissionszeitpunkt der Photonen bereits nicht mehr so dicht versammelt. Das letztere gilt auch für die uns näheren kosmischen Objekte. Außerdem sei hier angemerkt, daß Galaxien mit z > 1,25 erst in Zukunft zunehmend sichtbar werden.
4. Lichtlaufzeit in Abhängigkeit von Rotverschiebung und scheinbarer Helligkeit
Des weiteren lassen sich einfache Gleichungen für jeden beliebigen Emissionszeitpunkt der Photonen in Abhängigkeit von der Rotverschiebung bzw. der scheinbaren Helligkeit angeben.
Die vom Photon benötigte Laufzeit (look-back time) in Abhängigkeit von der beobachteten Rotverschiebung beträgt wegen Gleichung (I,7)
| (I,16) | 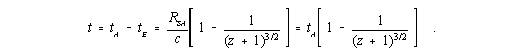
|
| (11) | 
|
|
Die Lichtlaufzeit als Funktion der scheinbaren Helligkeit wird mit den Gleichungen (I,18)
| (I,18) | 
|
| (12) | 
|
| (13) | 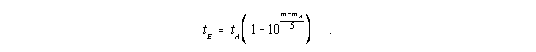
|
Literatur:
Haase, St.; www.xhaase.de (2001)
| zum nächsten Artikel | zurück zum Inhalt | zum vorhergehenden Artikel | zurück zur Artikelauswahl | Kontakt | Englisch |
Copyright by Steffen Haase, Leipzig, 1998 and 1999
Letzte inhaltliche Änderung: 23.12.2000
Letzte Schreibfehlerkorrektur: 13.05.2005