| zum nächsten Artikel | zum vorhergehenden Artikel | zurück zur Artikelauswahl | Kontakt | Englisch |
| Inhalt |
Zu einigen Problemen der modernen Kosmologie
V. Über die Rotverschiebung von Wellenlängen im Spektrum kosmischer Objekte
von St. Haase, Leipzig, BRD
Zusammenfassung:
Im vorliegenden Aufsatz wird über zwei eigentlich schon lange bekannte Rotverschiebungseffekte berichtet, die Anteile an den teilweise
beträchtlichen Rotverschiebungen erklären können, die heute bei extragalaktischen Objekten meßbar sind. Zum einen handelt es sich um die
Rotverschiebung von Spektrallinien durch sehr kompakte Himmelskörper, die mit Hilfe der äußeren Schwarzschild-Metrik beschrieben werden.
Zum anderen ergibt sich ein zweiter Effekt durch die Auswertung der inneren Schwarzschild-Metrik. Speziell diesem zweiten Effekt sollten
Photonen, die einen weiten Weg durch das mit Materie gleichmäßig erfüllte Universum zurücklegen, zusätzlich zum Expansionseffekt
unterliegen. Dieser zweite Rotverschiebungseffekt kann mühelos einen Anteil von zi £ 5,43 von der kosmischen Gesamtrotverschiebung erklären.
Hierdurch ergibt sich eine einfache Erklärung für die bisher gefundene Rotverschiebungsgrenze der Galaxien von etwa z » 6,68.
Abstract:
In the proposed essay two for a long time actually well-known red shift effects are reported, which can explain some of the in part considerable red shifts, which are measurable with extragalactic objects today. On the one hand it concerns the red shift of spectral lines by very compact celestial bodies, which are described with the help of the outside Schwarzschild metric. On the other hand a second effect arises as a result of the analysis of the internal Schwarzschild metric. Particularly photons, which travel a far way across the universe filled evenly with matter, should be subject to this second effect in addition to the expansion effect. This second red shift effect can easily explain some of zi £ 5.43 of the total cosmic red shift. Thereby we get a simple explanation for the red shift boundary of galaxies of about z » 6.68 found so far.
Key words: cosmology, red shift, Hubble parameter, Schwarzschild metric, universe
1. Einleitung
In den Teilen I, II und IV dieser Artikelserie [St. Haase, 2001] ergaben sich Hinweise darauf, daß eigentlich keine extragalaktischen Rotverschiebungen von Wellenlängen meßbar sein sollten, die größer als z » 1,25 sind. Da dies dennoch der Fall ist, muß nach weiteren theoretischen Möglichkeiten gesucht werden, die diese Erscheinung ergänzend beschreiben können. Zu diesem Zweck werden hier zwei Rotverschiebungseffekte diskutiert, die sich durch die strenge kugelsymmetrische Lösung der Einsteinschen Feldgleichungen ergeben. Beide Rotverschiebungseffekte gehen auf K. Schwarzschild [1916] zurück.
Die folgenden Ausführungen beruhen auf der nicht-euklidischen Geometrie, obwohl beide Rotverschiebungseffekte auch im Rahmen der Newtonschen Näherung ableitbar sind.
2. Rotverschiebung im kugelsymmetrischen Gravitationsfeld einer Zentralmasse M
Die Einsteinschen Vakuum-Gleichungen für kugelsymmetrische Verhältnisse werden durch die sogenannte äußere Schwarzschild-Metrik [K. Schwarzschild, 1916a]
| (1) | 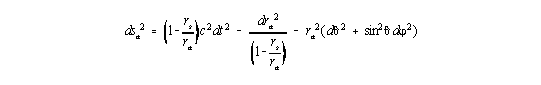
|
gelöst. Hier ist rs = 2MG/c2 (mit Zentralmasse M und Newtonscher Gravitationskonstante G) der Schwarzschild-Radius. Die Größen ra, j, J und t sind die Schwarzschild-Koordinaten, denen wegen der geometrischen Interpretation der Allgemeinen Relativitätstheorie (ART) keine unmittelbare physikalische Bedeutung zukommt. Das Quadrat der Eigenzeit ist gegeben durch
| (2) | 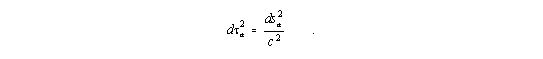
|
Aufgrund des unterschiedlichen Zeitverlaufes an verschiedenen, aber sonst festen (dra = dj = dJ = 0) Raumpunkten des Gravitationfeldes
| (3) | 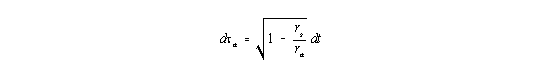
|
kommt es beim radialen Durchlaufen des Gravitationsfeldes zu einer Frequenzverschiebung einer elektromagnetischen Welle zwischen den Raumpunkten 1 und 2
| (4) | 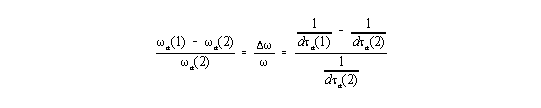
|
d.h.
| (5) | 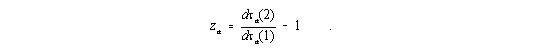
|
Für ein schwaches Gravitationsfeld folgt aus (3)
| (6) | 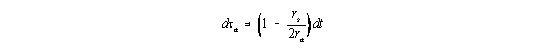
|
und damit für die Rotverschiebung za
| (7) | 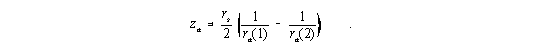
|
Dieser nur von der Potentialdifferenz zwischen zwei Raumpunkten abhängige Effekt ist als Rotverschiebung von Spektrallinien im Schwerefeld der Erde bestens bestätigt worden (Pound und Repka, 1960).
Bei Himmelskörpern mit einer radialen Ausdehnung von ra --> rs (etwa Neutronensterne) muß selbstverständlich die ungenäherte Gleichung
| (8) | 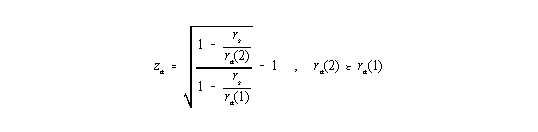
|
zur Anwendung kommen. Wenn ein Stern oder ein Sternsystem aus sehr großer Entfernung betrachtet wird, kann ra(2) » ¥ gesetzt werden, und es ergibt sich hierfür
| (9) | 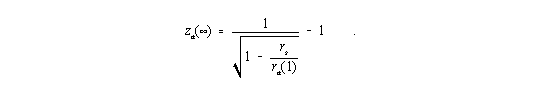
|
Die Radialkoordinate ra hat nur in großen Abständen von der Zentralmasse M die unmittelbare Bedeutung einer Entfernung. Der tatsächliche radiale Abstand ist in der Allgemeinen Relativitätstheorie definiert gemäß
| (10) | 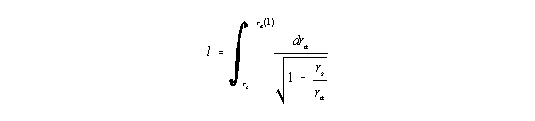
|
und ist stets etwas größer als ra. Die Integration in den angegebenen Grenzen führt auf
| (11) | 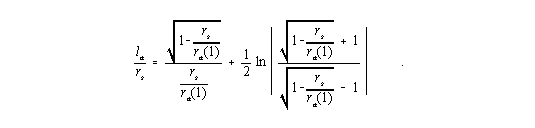
|
Die Verbindung der Gleichungen (9) und (11) ergibt eine Beziehung, die die Abhängigkeit des Verhältnisses la/rs von za(¥) zu bestimmen gestattet. Das Resultat ist
| (12) | 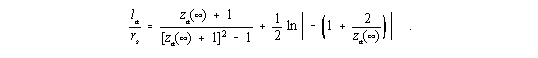
|
Der Abstand la kann nun einfach als Ort der Photonenemission (Oberfläche des leuchtenden Objektes) betrachtet werden, und der Beobachter befindet sich näherungsweise im Unendlichen. Nähert sich die Größe des kosmischen Objektes dem Schwarzschild-Radius, bemerkt dieser ferne Beobachter eine wachsende Rotverschiebung der Spektrallinien. Wenn aber das kosmische Objekt eine große Ausdehnung besitzt (la >> rs), wird die Rotverschiebung entsprechend klein.
Bei genauer Betrachtung der Gleichung (11) ist ersichtlich, daß für ra = rs la = 0 gilt; der Bezugspunkt des räumlichen Abstandes liegt - bezogen auf die ursprüngliche Schwarzschild-Radialkoordinate - beim Schwarzschild-Radius selbst. Das kann als deutlicher Hinweis für eine minimale Größe einer Zentralmasse M gewertet werden, denn eine kleinere untere Grenze als rs beim Integral (10) ist physikalisch sinnlos. Außerdem sollten die in den Gleichungen auftretenden Wurzeln stets reell sein.
Der hier abgeleitete Effekt, der nur vom Verhältnis von Ausdehnung und Schwarzschild-Radius des betrachteten kosmischen Objektes abhängt, ist selbst für Neutronensterne mit la/rs » 0,3 noch sehr klein. Sehr stark rotverschobene extragalaktische Objekte müßten äußerst kompakt sein, wenn die Rotverschiebung aufgrund der äußeren Schwarzschild-Metrik wirksam werden soll.
3. Rotverschiebung im Gravitationsfeld einer homogenen kugelsymmetrischen Materieverteilung
Ebenfalls auf K. Schwarzschild [1916b] geht die Metrik für das Innere einer Massenkugel mit homogener und zeitlich konstanter Massendichte rH zurück:
| (13) | 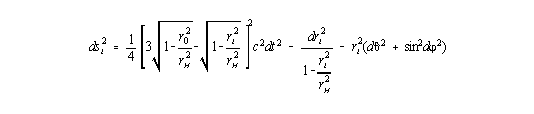
|
mit
| (13a) | 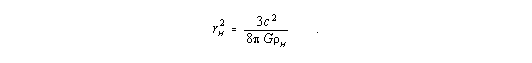
|
Hierbei ist rH der Hubble-Radius. Er drückt die maximale Reichweite von Wechselwirkungen innerhalb der betrachteten Materiekugel aus und kann auch als Ereignishorizont interpretiert werden. Die Koordinate r0 ist der radialen Ausdehnung des Systems proportional, und es gilt ri £ r0 £ rH. Die Größe ri ist wieder die Schwarzschild-Radialkoordinate, die auch hier in den wirklichen physikalischen Abstand umgerechnet werden muß.
Im folgenden wird ohne Einschränkung der Allgemeinheit r0 = rH angenommen, d.h. das betrachtete kugelförmige System ist gerade so groß, wie es der Hubble-Radius erlaubt. Die Rechnung, die zur Gleichung für die Rotverschiebung von Wellenlängen innerhalb einer kugelförmigen Materieverteilung führt, erfolgt analog dem im vorangegangenen Abschnitt gegangenen Weg und liefert das Ergebnis
| (14) | 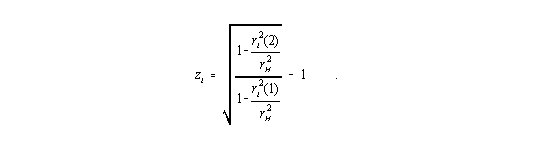
|
Der tatsächliche physikalische Abstand berechnet sich nach
| (15) | 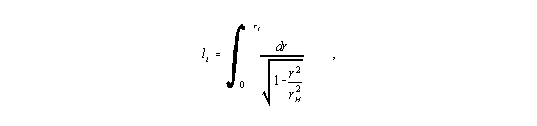
|
d.h. es wird
| (16) | 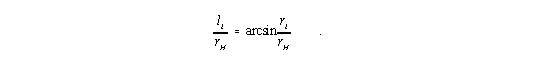
|
Für zi ergibt sich somit
| (17) | 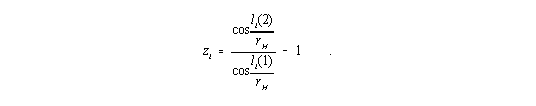
|
Aus Gleichung (16) folgt noch
| (18) |
Hier ist lH der physikalisch richtige Hubble-Radius.
Eine Rotverschiebung ergibt sich nur, wenn sich die Lichtquelle am Ort li(1) befindet, und der Beobachter an den Ort li(2) versetzt wird. Der größte Wert für eine Rotverschiebung von Wellenlängen innerhalb einer Materiekugel wird erreicht, wenn sich der Beobachter im Zentrum der betrachteten Kugel befindet, und das Photon auf der Oberfläche des Systems emittiert wird:
| (19) | 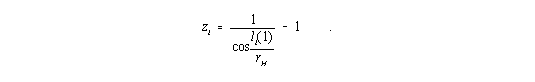
|
In diesem Fall wird zi = ¥. Für Lichtteilchen, die einen kürzeren Weg zum Beobachter zurücklegen, ist die Rotverschiebung entsprechend kleiner.
Anzumerken ist, daß im Rahmen der inneren Schwarzschild-Metrik periodische Vorgänge für große li(1) die höhere
Frequenz aufweisen, als die für kleinere li(1). Dies ist in guter Übereinstimmung mit der äußeren Schwarzschild-Metrik (Anschlußbedingung an den Oberflächen die durch rS und rH beschrieben werden).
Zur Rotverschiebung durch die kosmologische Expansion kommt also ein weiterer Anteil hinzu. Dieser wird durch die Bewegung von Photonen innerhalb einer statischen Materiedichte verursacht. Dieser Rotverschiebungseffekt ist in ähnlicher Form vorhanden, wenn sich die Materiedichte und damit auch der Hubble-Radius mit der Zeit ändern.
4. Der Vergleich mit den astrophysikalischen Meßwerten
Wie wir aus Teil IV dieser Aufsatzreihe [Haase, 2001] wissen, expandiert das Universum wegen der Begrenzung sämtlicher Geschwindigkeiten auf die des Lichtes erst seit etwa texp = 7,37 x 109 Jahren. Die heute am meisten rotverschobenen Photonen sind etwa diesen Zeitraum im Universum unterwegs gewesen. Während dieser Zeit dehnte sich das Universum so aus, daß die ursprünglich vorhandene Schwarzschild-Dichte rS = 11,4 rA bis heute auf den Wert rA = 7,3 x 10-30g cm-3 gesunken ist. Diese beiden Werte der Massendichte können für eine einfache Abschätzung der durch die innere Schwarzschild-Metrik vorausgesagten maximalen Rotverschiebung benutzt werden. Dies ist selbstverständlich nur eine Näherung, weil sich die Photonen wegen der Expansion des Universums nicht in einer zeitlich konstanten Materiedichte bewegt haben. Zur Abschätzung der oberen Grenze der Rotverschiebung nehmen wir zuerst an, daß die Massendichte im Universum die ganze Zeit rS betrug. Dann wäre die Rotverschiebung, die sich über die Gleichung (19) hierfür ergeben würde, nicht brauchbar, weil der zurückgelegte Lichtweg li unpassend größer als der zur Dichte rS gehörige Hubble-Radius rH wäre [sie wäre offenbar "mindestens" unendlich; :-)]. Dieses Ergebnis ist vollkommen in Ordnung, da die Dichte während der Lichtlaufzeit fast immer geringer als rS war. Jetzt nehmen wir an, daß die Photonen die ganze Zeit in einem Universum unterwegs waren, das immer die heutige Dichte rA hatte. In diesem Fall liefert die Gleichung (19) den Wert zi = 0,1211. Dies ist nun ein sicherer unterer Grenzwert für den Beitrag der inneren Schwarzschild-Metrik zur kosmologischen Rotverschiebung. Dieser Wert ist auf jeden Fall zu klein, da die Dichte vom Universum beinahe immer größer war, als sie heute ist. Eine zu erwartende mittlere Massendichte muß sinnvollerweise zwischen den beiden Dichten rS und rA liegen. Benutzen wir deshalb als weitere Abschätzmöglichkeit den Mittelwert aus beiden Dichten, ergibt sich bereits ein Rotverschiebungsbeitrag von zi = 1,5519. Aus der Literatur ist bekannt, daß die größte heute gemessene Rotverschiebung einer Galaxie den Wert z = 6,68 beträgt. Das Expansionsmodell vom Universum kann davon maximal z = 1,25 beitragen. Hierdurch verbleibt ein Rest von z = 5,43, den die innere Schwarzschild-Metrik beisteuern müßte. Die Frage nach der zugehörigen durchschnittlichen Massendichte wird mit <rH> = 9,09 rA beantwortet. Dies ist ein sehr guter Wert, weil er in vernünftiger Weise zwischen den beiden genannten Dichtegrenzwerten rS und rA liegt.
5. Zusammenfassung
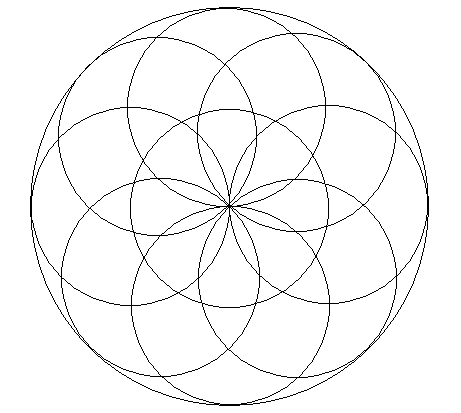
Zum Schluß soll noch ganz allgemein auf die Struktur des Universums eingegangen werden. Dazu zeigt die Abb.1 . zweidimensionale Projektionen von 8 Massenkugeln, die jeweils der Friedmann-Gleichung genügen. Die acht hier gewählten Massenkugeln stehen stellvertretend für eine unendliche Anzahl solcher gedanklich aus dem Universum herausschneidbaren Kugeln. Der Beobachter befindet sich in der Mitte der Abbildung. Es ist zu erkennen, daß sich der Beobachter auf den einzelnen Oberflächen der Materiekugeln befindet, die sich überlappende Teile vom Gesamtuniversum repräsentieren. Das Gesamtuniversum hat mindestens die Größe der äußeren Kugel. In welche Richtung der Beobachter auch schauen mag, er blickt immer in Richtung eines Kugelmittelpunktes, der sich stets im Abstand RSA = DA befindet. Durch den Aufenthalt des Beobachters auf den Oberflächen der Kugeln wird die Rotverschiebung gemäß der Gleichung (I,18) wirksam, die die Friedmannsche Expansion des Universums beschreibt. Aber gleichzeitig befindet sich der Beobachter auch im Zentrum der inneren kleinen Materiekugel. Hierdurch wird die Rotverschiebung gemäß der Gleichung (19) wirksam. Auch diese Kugel dehnt sich gemäß der Friedmann-Gleichung aus. Ihr Radius entspricht dem Ereignishorizont, über den der Beobachter nicht hinaussehen kann. Photonen vom Rand dieser Kugel sind unendlich rotverschoben. Diese unendliche Rotverschiebung kann heute (noch) nicht beobachtet werden, da das Universum erst seit ca. texp = 7,37 x 109 Jahren expandiert. Dies begrenzt die Rotverschiebung auf z » 7, wenn beide Rotverschiebungseffekte summiert werden. Hierdurch ergibt sich die Begrenzung der Meßwerte im Hubble-Diagramm in bezug auf die Ordinate lg( cz ). Die Begrenzung der Meßwerte im Hubble-Diagramm bezüglich der Abszisse m wird durch die scheinbare Grenzhelligkeit mA verursacht. Objekte, die sich im Hubble-Diagramm weiter rechts (größere m-Werte) befinden, sind von Natur aus lichtschwächer, als es die mittlere absolute Helligkeit angibt.
Vielleicht mag es etwas merkwürdig anmuten, daß sich der Beobachter auf den Oberflächen von Materiekugeln und gleichzeitig auch im Zentrum einer gleichgearteten Kugel befindet. Diese Aussage sollte nicht sonderlich verwundern, da die Quantentheorie ein ähnliches Interpretationsproblem kennt: Man kann bis zum heutigen Tag nicht entscheiden, ob ein quantentheoretisches Objekt ein Teilchen oder eine Welle ist. Es ist offenbar beides. Aus diesem Grund ist es denkbar, daß wir uns auch an das hier skizzierte neue Bild vom Universum gewöhnen werden!
Literatur:
Haase, St.:
www.xhaase.de (2001)
Pound, R. W. und Repka, G. A.:
Phys. Rev. Letters 4 (1960), S.337
Schwarzschild, K.:
Sitz.-Ber. Preuß. Akad. Wiss. (1916a), S.189
Schwarzschild, K.:
Sitz.-Ber. Preuß. Akad. Wiss. (1916b), S.424
|
| Abb. 1:
Die Abbildung zeigt die einfache Struktur des Universums, die sich auf Grund der in dieser Artikelserie entwickelten physikalischen Modellvorstellung zwanglos ergibt. Weitere Erläuterungen hierzu befinden sich im Text. |
| zum nächsten Artikel | zurück zum Inhalt | zum vorhergehenden Artikel | zurück zur Artikelauswahl | Kontakt | Englisch |
Copyright by Steffen Haase, Leipzig, 1998 and 1999
Letzte inhaltliche Änderung: 31.12.2000
Letzte Schreibfehlerkorrektur: 21.05.2005