
| zum nächsten Artikel | zum vorhergehenden Artikel | zurück zur Artikelauswahl | Kontakt |
| Inhalt |
Zu einigen Problemen der modernen Kosmologie
III. Über die mittlere Größe extragalaktischer Objekte
von Steffen Haase, Leipzig, BRD
Zusammenfassung:
Mit Hilfe neuer Winkelausdehnungs-Helligkeits- und Winkelausdehnungs-Rotverschiebungs-Relationen im euklidischen Raum kann die mittlere lineare Ausdehnung von Galaxien mit d » 30 kpc angegeben werden. Ein Minimum in der Winkelausdehnungs-Rotverschiebungs-Relation für z » 1,25 wird nicht gefunden.
Abstract:
With the help of new angular size-magnitude and angular size-redshift relations in the euclidean space the mean linear size of galaxies can be stated to d » 30 kpc. In the angular size-redshift law a minimum for z » 1.25 cannot be found.
Key words: cosmology, angular size, galaxies, redshift
1. Zusammenstellung einiger Gleichungen
Eine weitere für die Kosmologie interessante astrophysikalische Größe ist die lineare Ausdehnung extragalaktischer Objekte. Da diese Größe meßtechnisch nicht unmittelbar zugängig ist, wird im allgemeinen der Umweg über die Winkelausdehnung gegangen. Für die Winkelausdehnung eines beliebigen Objektes gilt ganz einfach
| (1) | 
|
| (I,16) | 
|
| (2) | 
|
Zum Vergleich sei hier die entsprechende Gleichung für den flachen Raum (q0 = 1/2) aus der Literatur (s. z.B. A. Sandage, 1995) angeben:
| (zzz) | 
|
Während die Gleichung (2) einen Zusammenhang der Form j = j(z; d/DA) liefert, ergibt sich die Winkelausdehnungs-Helligkeits-Relation j = j(m; d/DA, mA) über
| (3) | 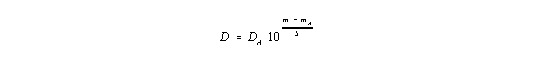
|
| (4) | 
|
| (5) | 
|
Damit steht eine Reihe von Gleichungen zur Verfügung, deren Richtigkeit durch den Vergleich mit vorhandenen astrophysikalischen Meßergebnissen geprüft werden kann.
2. Der Vergleich mit den astrophysikalischen Messungen
Im folgenden wird stellvertretend für die Vielzahl von j-m-Diagrammen der Literatur die Zusammenstellung von J. Huchra u.a. (1983) herangezogen, um den Parameter d/DA zu bestimmen. Zur Auswertung dieses Galaxien-Kataloges wurden wegen der m-Begrenzung des CfA-Kataloges gleichgroße m-Intervalle gebildet und hierzu die m- und j-Mittelwerte. Das Ergebnis zeigt Abb.1 . Die Angleichung der Theorie an die bestangepaßte Kurve durch die Mittelwerte führt auf d/DA = 9,357 x 10-6. Hiermit ergibt sich wegen DA = 3206 Mpc eine durchschnittliche lineare Ausdehnung der CfA-Galaxien von d = 30 kpc (entsprechend der im CfA-Katalog benutzten Definition der Winkelausdehnung). Zum Vergleich: Die Literatur gibt für die Milchstraße 34 kpc als Durchmesser an.
Generell gestattet die Gleichung (4) die Berechnung aller linearen Ausdehnungen von Sternsystemen, wenn deren scheinbare Helligkeit und die zugehörige Winkelausdehnung gemessen werden. Die Anwendbarkeit der Gleichung (4) setzt aber voraus, daß sich die linearen Ausdehnungen der kosmischen Objekte im Verlauf der Entwicklung des Universums nicht verändert haben dürfen, da die abgeleiteten Gleichungen Änderungen dieser Größe nicht berücksichtigen. Außerdem müßten alle betrachteten Systeme eine gleichgroße absolute Helligkeit besitzen, doch in Wirklichkeit streut diese innerhalb eines großen Bereiches.
Die Abb.2 zeigt die Anwendung der Gleichung (2) auf die Galaxiendaten nach S. Bardelli u.a. (1995). Dieser Katalog ist in bezug auf die Winkelausdehnung begrenzt. Aus diesem Grund wurden j = 0,5'-Intervalle und die zugehörigen j- und cz-Mittelwerte gebildet, wobei die Größe 0,5' willkürlich gewählt wurde. Mittelwerte mit weniger als 3 Objekten wurden nicht in das Bild aufgenommen, um statistische Verfälschungen möglichst zu vermeiden. So ergibt sich hier ebenfalls das Verhältnis d/DA = 9,357 x 10-6. Die mittlere lineare Ausdehnung dieser Galaxien ist demnach mit dem Wert der CfA-Objekte unmittelbar vergleichbar.
Das oben ausgewertete Datenmaterial gibt wegen den relativ kleinen Rotverschiebungen keine Auskunft über das Vorhandensein des von den Astrophysikern schon lange gesuchten Minimums der Winkelausdehnung bei z = 1,25 [vgl. mit A. Sandage (1988), K.I. Kellermann (1993a, b) und L.I. Gurvits (1994)]. Die Gleichung (2) sagt auch kein solches Minimum voraus, wie die Anwendung der Differentialrechnung sofort bestätigt. Die Winkelausdehnung wird für hinreichend große Rotverschiebungen unabhängig von z und strebt für z -> ¥ gegen d/DA. Das Datenmaterial von K.I. Kellermann (1993a, b) und L.I. Gurvits (1994) scheint auf das Existieren eines Minimums hinzuweisen, aber die von P. Coles u.a. (1994) erwähnte genauere Analyse dieser Meßergebnisse weist auf eine eher horizontal auslaufende bestangepaßte Kurve hin, die wahrscheinlich mit dem hier vorgestellten theoretischen Ansatz im Einklang steht.
Für die Abb.3 wurde die Tabelle der größten Winkelausdehnungen (LAS: largest angular size) von Radiogalaxien von K. Nilsson (1993) verwendet und die Theorie entsprechend Gleichung (2) angepaßt. Hierzu wurde das in der Abbildung auch angegebene Polynom 5. Grades benutzt, das sich im Zentrum des Datenmaterials gut an die theoretische Kurve anschmiegt. Es wird kein Minimum im lg(LAS)-lg(cz)-Diagramm gefunden. Die gemessenen Werte kommen für größere Rotverschiebungen eher unterhalb der neuen theoretischen Kurve (untere ausgezogene Linie) zu liegen und weichen von dieser wesentlich weniger ab, als von der in der Literatur zu findenden Theorie. Die Lage der Meßpunkte für große Rotverschiebungen könnte Entwicklungseffekten zugeschrieben werden: Die kosmischen Objekte waren in der Frühzeit möglicherweise generell kleiner als später bzw. heute. Ein solcher Effekt wurde aber bei der Ableitung der hier vorgestellten Gleichungen nicht berücksichtigt.
Literatur:
Bardelli, S. und Zucca, E.:
Astronomische Nachrichten, 316 (1995) 1, S.39
Coles, P. und Ellis, G.
Nature, 370 (1994), S. 609
Gurvits, L.I.:
The Astrophysical Journal, 425 (1994) S.442
Haase, St.: www.xhaase.de (2001)
Huchra, J.; Davis, M.; Latham, D. und Tonry, J.:
The Astrophysical Journal Supplement Series, 52 (1983), S.89
Kellermann, K.I.:
Nature, 361 (1993a), S.134
Kellermann, K.I.
Sub-arcsecond Radio Astronomy, ed. by R.J.Davis and R.S.Booth,
Cambridge Univ. Press, (1993b), page 386
Nilsson, K.; Valtonen, M.J.; Kotilainen, J. und Jaakkola, T.:
The Astrophysical Journal, 413 (1993) S.453
Sandage, A. R.:
in Sandage, A.; Kron, R.G. und Longair, M.S.:
The Deep Universe, Springer-Verlag, 1995,
(Saas-Fee Advanced Course 23, Lecture Notes 1993,
Swiss Society for Astrophysics and Astronomy,
Herausgeber: B.Binggeli und R.Buser)
Abbildungen:

|
| Abb.1:
lgj-m-Diagramm nach J. Huchra u.a. (1983). Die theoretische Kurve (durchgezogene Linie) liegt deutlich auf der bestangepaßten Kurve (gestrichelte Linie) durch die Intervall-Mittelwerte (Kreise) der Galaxien (Quadrate). Für die theoretische Kurve gilt DA = 3206 Mpc. Die Mittelwerte sind durch Kreise dargestellt. |

|
| Abb.2:
lgj-lg(cz)-Diagramm nach S. Bardelli u.a. (1995). Die theoretische Kurve (durchgezogene Linie) paßt sehr gut zu den gebildeten Mittelwerten (Kreise). Für die Kurve gilt ebenfalls DA = 3206 Mpc. Die gestrichelte Linie ist die bestangepaßte Kurve durch die Intervall-Mittelwerte. |

|
| Abb.3:
lg(LAS)-lg(cz)-Diagramm nach K. Nilsson u.a. (1993). Die punktierte Linie entspricht der Theorie aus der Literatur. Die durchgezogene Linie repräsentiert die hier dargestellte Theorie. Die gestrichelt Linie entspricht dem bestangepaßten Polynom 5. Grades. Weitere Erläuterungen hierzu finden sich im Text. Auch hier wurde DA = 3206 Mpc verwendet. |
| zum nächsten Artikel | zurück zum Inhalt | zum vorhergehenden Artikel | zurück zur Artikelauswahl | Kontakt |
Copyright by Steffen Haase, Leipzig, 1998 and 1999
letzte inhaltliche Änderung: 15.04.2000
letzte Schreibfehlerkorrektur: 21.05.2005