| to the next article | back to the privious article | back to the article selection | get in touch |
| TABLE OF CONTENTS: |
ABOUT SEVERAL PROBLEMS OF MODERN COSMOLOGY
II. ABOUT THE NUMBER OF COSMIC SYSTEMS IN THE UNIVERSE
Steffen Haase, Leipzig, Germany
ABSTRACT
For the euclidean space new equations are given regarding the dependence of the number of extragalactic objects on redshift and apparent magnitude. For the number of extragalactic systems dN within a redshift interval dz the maximum is at z = 0.6915. The average redshift is expected to be at <z> » 0.2189, assuming that the maximum redshift depending on the distance is zmax » 5. Since hardly any redshift with z ³ 5 can be found, the formation of galaxies could possibly have started at the corresponding moment. The finding of <z> with the help of measuring techniques would define the beginning of the formation of galaxies in the redshift space.
Subject headings: cosmology: distance scale --- cosmology: theory --- galaxies: distances and redshifts --- galaxies: statistics --- quasars: general
1. PRELIMINARY REMARKS
The dependence of the number of extragalactic objects on the redshift z and the apparent magnitude m respectively belongs to classical tests of theoretical cosmology. Both effects shall be considered more detailed here.
In part I of this article series (Haase 2000) we have given the following easy relation for the apparent radial distance D between any two cosmic objects
| (I,6) | 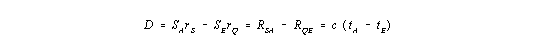
|
2. DERIVATION OF THE NUMBER-EQUATIONS N(z) and N(m)
The sphere volume V in the euclidean space a photon goes through radially is given by
| (1) | 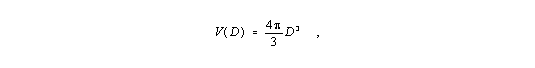
|
| (I,16) | 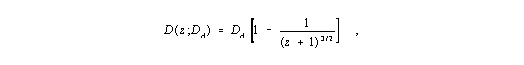
|
| (2) | 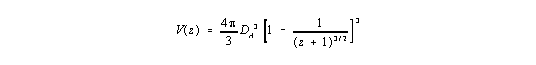
|
| (3) | 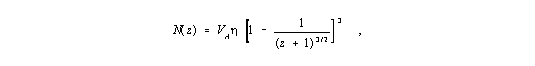
|
| (4) | 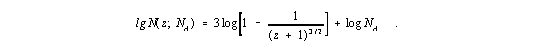
|
For comparison the equation derived in the literature for the flat redshift space (q0 = 1/2) is given (see e.g. A. Sandage 1995):
| (yyy) | 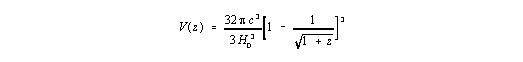
|
The differentiation of the count redshift relation with respect to z
| (5) | 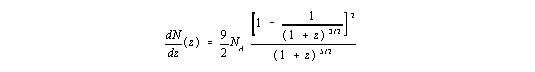
|
Besides it is useful, to calculate the expected mean value <z> of the redshifts, to compare it with the measuring results. Using the mean value theorem of the integral calculation equation (5) gives
| (6) | 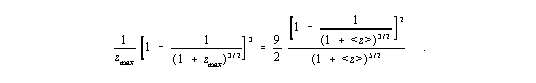
|
The occurrence of a limited redshift also implies a limit mmax of the apparent magnitude because of the Hubble
law (I,18), for which m £ mmax £ mA. For example mmax = 22.47 for zmax = 5, whereas mmax = 22.33 for zmax » 3,
assuming mA = 22.62 is taken as base. Then the low magnitudes of galaxies beyond mmax are not only determined
by the distance of this systems.
For the count magnitude relation we get
| (7) | 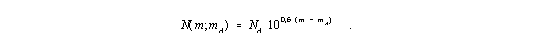
|
The derivative of N(m) with respect to m is
| (8) | 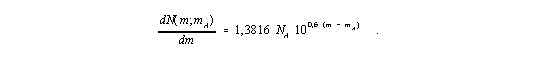
|
3. COMPARISION WITH THE ASTROPHYSICAL MEASUREMENTS
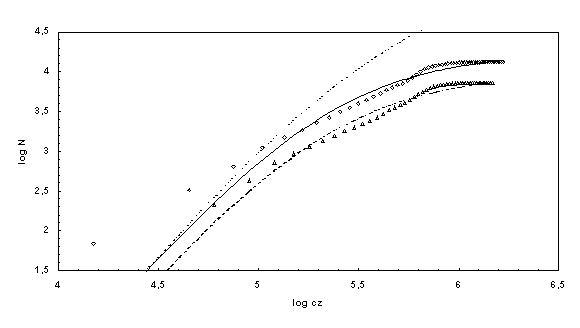
Unfortunately there is no a complete measurement series for the number of galaxies which is limited by the redshift. We therefore assume that the quasars which were found so far are uniform distributed over the whole sky. According to this assumption the measurement data by Véron-Cetty et al. (2000) and for comparison the catalog No.7158 of the Astronomical Data Center (Hewitt & Burbidge 1993) were used to fit the theory with the observations. The result is shown in Fig.4. The parameter NA was always chosen so, that the theoretical curves just meet the measuring series for the greatest measured redshifts. Hereby we get the values NA » 16500 for the year 2000 and NA » 8993 for the end of the year 1993. The equation (4) always describes really observed data very well. If the assumption above is quite reliable, we might think, that there do not exist considerable more than about 2 x 104 quasars, of which 13214 quasars were already known in march of the year 2000. However we can also see that NA is increasing as the number of years is increasing. Fig.4 shows a significant surplus of quasars with large redshift, a lack of this objects for mean z and again a surplus for small redshifts. The dotted line corresponds to equation (yyy). As we can see, the corresponding theoretical derivation is not suitable for explaining the measured data.
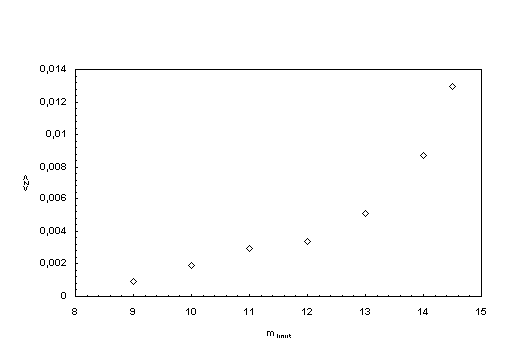
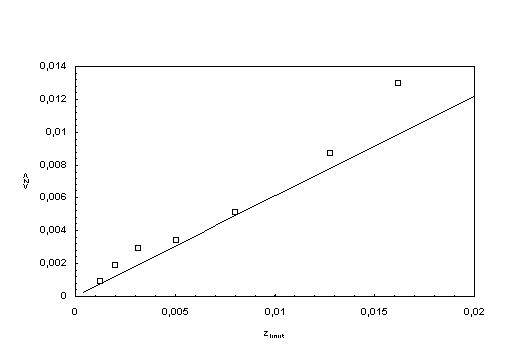
Using the data material from Huchra et al. (1983), to form redshift mean values <z> up to any different limits mlimit of the apparent magnitude, gives Fig. 5 . It is clear, that this mean value increases as the limit mlimit increases. Most probably this increasing continuous up to the apparent limit magnitude mmax and mA, respectively, and stops there. Conversion on trial of limits of the apparent magnitude mlimit which were used in Fig.5 to the redshift limits zlimit with the help of the Hubble law (I,18) leads to Fig. 6 . We can see the trend the theory is asking for. Since the used measured values are not really a series which is limited by z we cannot expect a complete correspondence between the theory and the measured results. Therefore it is necessary, to provide complete measuring series in z, to really make statements about the time of origin of the first galactic systems.
A further note of the increasing of the mean redshift is for example also given in Kron (1993, Fig.7.1.).
However there the mean redshift is evaluated within intervals of the apparent magnitude BJ. If no m-intervals are
used, but <z> is formed integrally up to certain limited apparent magnitudes, then it is clear, that these mean values
are always below the greatest value given by Kron (1993), because then many objects with very small redshifts
come into consideration. The fall of the mean redshift is strengthened as well by the fact, that there are hardly
objects beyond BJ = 27 [compare with Yoshii (1993, Fig. 5a)], which could pull up the mean value. This
corresponds to the expectation of the proposed theory, that according to equation (5) only a few objects are
expected for large z. The mean value of the redshift is therefore relative small. The measuring results really point
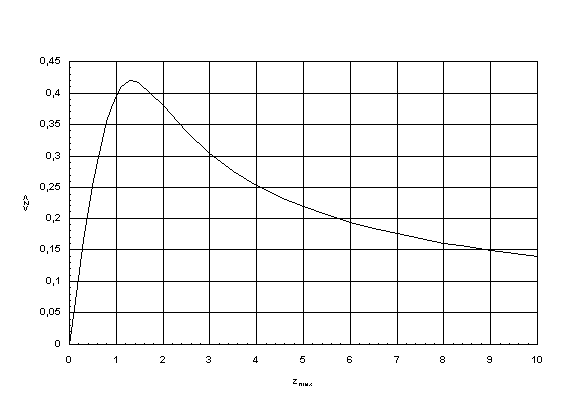
at a small redshift mean value. Equation (6) expects a possible maximum value of <z>max = 0.4192 for zmax = 1.3
(compare with Fig.3). For each other zmax the mean redshift <z> is always smaller.
Because of less data material being available to the author a conclusive evaluation of the count magnitude relations (7) and (8), respectively was not possible. Therefore it is just noted, that for example in the figures 5a to 5d from Yoshii (1993) the great lack of galaxies beyond certain apparent limit magnitudes is distinctly perceptible. To compare equation (7) with the measuring results, only objects, which are located with their apparent magnitude before this fraction point in the mentioned diagrams, can be considered because the galaxies behind have obviously a naturally lower magnitude and are therefore in this part of the diagram. Since their number is also missing to the left of the fraction point, the slope of the curve diminishes. Note also the occurrence of mmax £ mA , if a zmax exists. Hereby the fraction point, from which only a few objects will be found, will be shifted to smaller m-values, as expected else.
REFERENCES
Haase, St. 2000, www.xhaase.de
Hewitt, A., & Burbidge, G. 1993, ApJS, 87, 451
(NASA / Goddard Space Flight Center: Astronomical Data Center, Volume 2, catalog 7158)
Huchra, J., Davis, M., Latham, D. & Tonry, J. 1983, ApJS, 52, 89
Kron, R.G. 1995, in The Deep Universe, ed. A. Sandage et al., (Berlin: Springer-Verlag), 292
Sandage, A. R. 1995, in The Deep Universe, ed. A. Sandage et al., (Berlin: Springer-Verlag)
Véron-Cetty, M.-P. & Véron, P. 2000, "A Catalogue of Quasars and Active Nuclei", 9th edition, http://www.obs-hp.fr or A&AR (in press)
Yoshii, Y. 1993, ApJ, 403, 552
FIGURES:
|
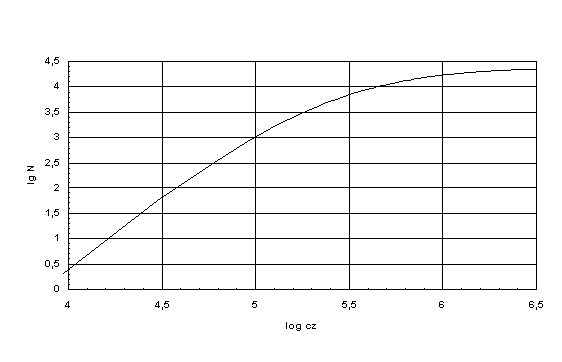
| Figure 1.
Count redshift relation according to equation (4). The curve was normalized to one square degree and NA was set to 109. For large redshifts the number of objects to be found increases insignificantly. |
|
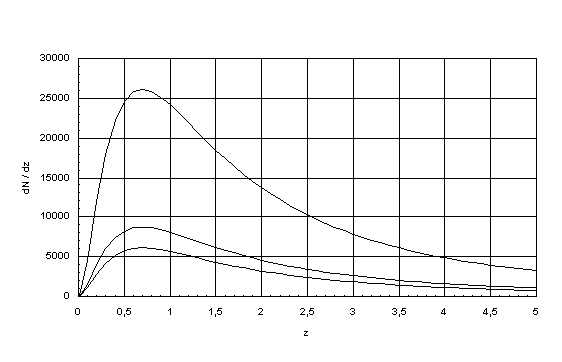
| Figure 2.
Differential number dN of cosmic objects in a redshift interval dz depending on the redshift for different NA. The values of NA were chosen to be 7 x 108, 1 x 109 and 3 x 109, respectively. For z » 0.7 we always have a maximum. |
|
| Figure 3.
Mean value <z> of the redshift as a function of a maximum possible redshift zmax. |
|
| Figure 4.
Comparison of the theory with the number of the quasars that were discovered until the end of 1992 (triangles) and March 2000 (diamonds), respectively according to the catalog No.7158 of the Astronomical Data Center (Hewitt & Burbidge 1993) and Véron-Cetty et al. (2000). The dotted line corresponds to the theoretical derivation that can be found in the literature. |
|
| Figure 5.
Mean redshift <z> up to chosen m-limits (according to Huchra et al. 1983). |
|
| Figure 6.
Mean redshift <z> up to calculated z-limits (measuring values according to Huchra et al. 1983). |
| to the next article | back to the table of contents | back to the privious article | back to the article selection | get in touch |
copyright by Steffen Haase, Leipzig, 1998 and 1999
last update: 04/15/2000
last correction of spelling mistakes: 05/22/2005