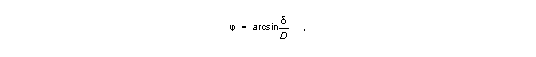
| to the next article | back to the privious article | back to the article selection | get in touch |
| TABLE OF CONTENTS: |
ABOUT SEVERAL PROBLEMS OF MODERN COSMOLOGY
III. ON THE MEAN SIZE OF COSMIC OBJECTS
Steffen Haase, Leipzig, Germany
ABSTRACT
Using new angular size-magnitude and angular size-redshift relations in the euclidean space we obtain a value of d » 30 kpc for the mean linear size of galaxies. A minimum for z » 1.25 in the angular size-redshift law cannot be found.
Subject headings: cosmology: distance scale --- cosmology: theory --- galaxies: distances and redshifts --- galaxies: fundamental parameters (radii)
1. COMPILATION OF SOME EQUATIONS
A further astrophysical quantity which is interesting for cosmology is the linear size of extragalactic objects. Since this quantity is not directly accessible with measurement technologies, the angular size is generally used. For any object it is
| (1) | 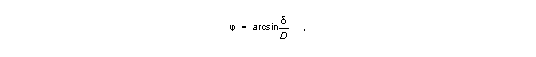
|
| (I,16) | 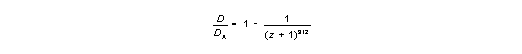
|
| (2) | 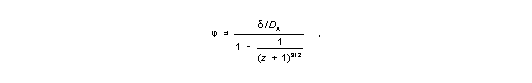
|
For comparison the appropriate equation for the flat space (q0 = 1/2) derived in the literature (s. e.g. A. Sandage, 1995) is:
| (zzz) | 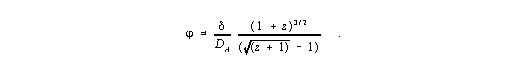
|
While equation (2) gives a relation of the form j=j (z; d/DA), the angular size-magnitude law j =j (m; d/DA, mA) is using
| (3) |
| (4) | 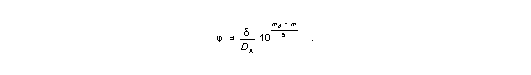
|
| (5) | 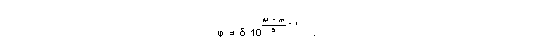
|
Therefore a whole a string of equations is available, the correctness of which can be tested by comparing it with existing astrophysical measuring results.
2. COMPARISION WITH ASTROPHYSICAL MEASUREMENTS
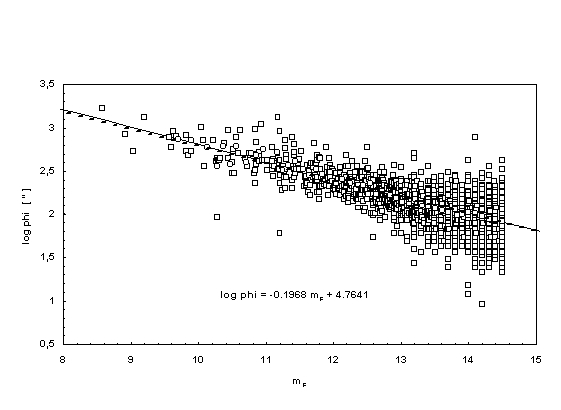
Acting for a multitude of j-m-diagrams in the literature in the following the compilation by Huchra et al. (1983) is used, to determine the parameter d/DA. For the evaluation of this galaxy catalogue equal m-intervals and corresponding m- and j-mean values were formed because of the m-limitation of the CfA catalogue. The result is shown in Fig.1 . Fitting the theory with the best fit through the mean values gives d/DA = 9.357x10-6. Thus because of DA = 3206 Mpc the mean linear size of the CfA galaxies is d= 30 kpc (according to the definition of the angular size used in the CfA catalogue). For comparison: The literature states a linear diameter of 34 kpc for the milky way.
In general equation (4) allows the calculation of all linear sizes of star systems, the apparent magnitude of which and the corresponding angular size is measured. However the application of equation (4) requires, that the linear diameters of the cosmic objects did not change during the development of the universe, because the derived equations do not consider changes of this size. Besides all of the considered systems should have an equal absolute magnitude, but in reality this scatters within a large area.
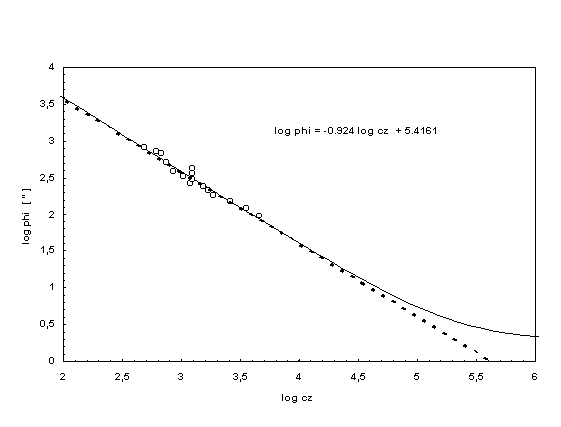
Fig.2 shows the application of equation (2) to galaxy data according to Bardelli & Zucca (1995). Related to the
angular size this catalogue is limited. Therefore j= 0,5'-intervals and corresponding j- and cz-mean values were
formed, where the size 0,5' was chosen randomly. Mean values with less than 3 Objects were neglected, to avoid
statistical falsification. Thus here we also have the proportion d/DA = 9.357x10-6. The mean linear size of these
galaxies is therefore directly comparable with the value of the CfA objects.
Because of the relative small redshifts the data evaluated above give no information about the existence of the minimum of the angular size at z = 1.25 astrophysicists are looking for for a long time [compare e.g. with Sandage (1988), Kellermann (1993a, b) and Gurvits (1994)]. Equation (2) also does not predict such a minimum, as the application of differential calculus confirms immediately. The angular size is independent of z for sufficiently large redshifts and approaches d/DA as z--> ¥. The data material due to Kellermann (1993a, b) and Gurvits (1994) seems to point at the existence of a minimum, but a more detailed analysis according to Coles & Ellis (1994) of this measuring results points at a curve of best fit which is rather parallel to the abscissa for large redshift values, which probably corresponds to the theoretical approach.
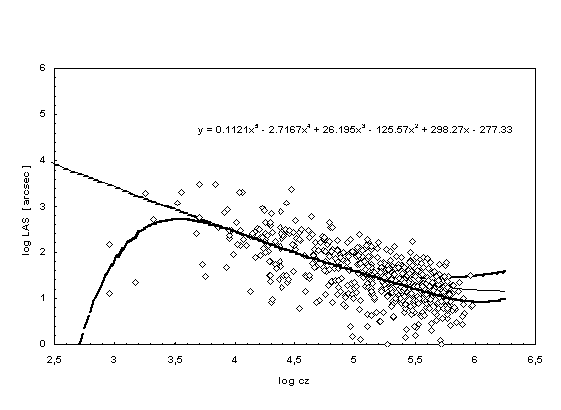
For Fig.3 the table of the largest angular sizes (LAS) of radio galaxies according to Nilsson (1993) was used and the theory corresponding to equation (2) fitted. Hereby a 5th order polynom also given in Fig.3 was used, which well approaches the theoretical curve in the center of the data material. No minimum is found in the log(LAS)-log(cz)-diagram. For larger redshifts the measured values lie more below the new theoretical curve (line below). The deviation is smaller than for the theory found in the literature. Development effects could be responsible for the location of the measuring points for large red shifts: Cosmological objects were probably smaller in sooner times than later and today, respectively. However such a effect was not considered while deriving the proposed equations.
REFERENCES
Bardelli, S., & Zucca, E. 1995, Astronomische Nachrichten, 316, 1, 39
Coles, P., & Ellis, G. 1994, Nature, 370, 609
Gurvits, L.I. 1994, ApJ, 425, 442
Haase, St. 2000, www.xhaase.de
Huchra, J., Davis, M., Latham, D., & Tonry, J. 1983, ApJS, 52, 89
Kellermann, K.I. 1993a, Nature, 361, 134
Kellermann, K.I. 1993b, in Sub-arcsecond Radio Astronomy, ed. R.J.Davis & R.S.Booth, (Cambridge: Cambridge Univ. Press), 386
Nilsson, K., Valtonen, M.J., Kotilainen, J., & Jaakkola, T. 1993, ApJ, 413, 453
Sandage, A. R. 1995, in "The Deep Universe", Saas-Fee Advanced Course 23, Lecture Notes 1993, edited by B. Binggeli and R. Buser, Springer Verlag
FIGURES:
|
| Figure 1.
Angular size-magnitude diagram according to Huchra et al. (1983). The theoretical curve (full line) lies significantly on the curve of best fit (dashed line) through the mean interval values (circles) of the galaxies (squares). The maximum distance DA = 3206 Mpc for the theoretical curve gives a mean linear size of = 0.03 Mpc. |
|
| Figure 2.
Angular-redshift diagram according to Bardelli & Zucca (1995). The theoretical curve (full line) corresponds very well to the formed mean values (circles). The best fit is represented by the dashed line. The maximum distance DA = 3206 Mpc for the theoretical curve gives a mean linear size = 0.03 Mpc as well. |
|
| Figure 3.
Largest angular size (LAS)-redshift diagram according to Nilsson et al. (1993). The new theory is represented by the full line and the old theory is given by the dotted line. The dashed line corresponds to the best fit (5th order polynom). For further explanations see text. Here the maximum distance DA = 3206 Mpc was also used and the linear size = 0.21 Mpc is provided for both theories. |
| to the next article | back to the table of contents | back to the privious article | back to the article selection | get in touch |
copyright by Steffen Haase, Leipzig, 1998 and 1999
last update: 04/15/2000
last correction of spelling mistakes: 05/22/2005