ABOUT SEVERAL PROBLEMS OF MODERN COSMOLOGY

I. ABOUT THE INTERPRETATION OF THE HUBBLE DIAGRAM

by Steffen Haase, Leipzig, Germany

1. DERIVATION OF THE REDSHIFT-MAGNITUDE RELATION

ABSTRACT

In the Euclidean space the way covered by a photon between an earthly observer and any galaxy is used as the dynamic distance between the two. Due to this approach a mean apparent limit magnitude of galaxies amounts to m_A = 22.62. This corresponds to a present maximum distance of D_A = 3206 Mpc, assuming that the mean absolute magnitude for galaxies is M = -19.91 in the first approximation. In this case the present Hubble parameter is H_A = 62.34 km s^-1 Mpc^-1 and the corresponding Hubble time t_H = 15.7 x 10⁹ years. The present density of the visible part of the universe is r_A = 7.3 x 10^-30g cm^-3. The mass corresponding to D_A amounts to M_U = 2.96 x 10⁵⁵g. For the mean absolute magnitude of the quasars M_Q = -23.07 is found.

Subject headings: cosmology: distance scale - cosmology: theory - galaxies: distances and redshifts - quasars: general

The easiest model for the universe results from the assumption of a homogeneous and isotropic distribution of matter in the universe in accordance with the cosmological principle. This assumption leads to the solution of Einstein's field equations with the help of the Robertson-Walker metric (RWM)

(1)

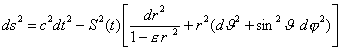
where S(t) denotes the time depending scale factor (also called radius of the universe) and c the speed of light. The curvature constant e can be ±1 or 0. The consideration Consideration of the dimensions shows that S can be measured in centimeter or Mpc. The comoving radial distance coordinate r as well as e are without dimension.

In the following the curvature constant e is always set to be zero always. Therefore the further considerations are only valid for the case of the flat Euclidean space. This procedure is justified by the good correspondence between the theoretical results and the measuring results of astrophysics which is shown in section 2.

For time-dependent measurable distances the RWM delivers

(2)

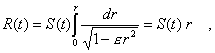
if e = 0 is taken into account. R(t) = S(t)r describes the physical distance from the coordinate origin r = 0 and the dimension of r is also that of a length. The change of the speed of distance changingis calculated to by dR/dt

(3)

The last equals sign is valid because of dr/dt = 0 for the extra galactic systems which forms the substratum of the universe. These cosmic objects don't show any proper motions, i.e. they rest in the substratum. This is an immediate result of the cosmological principle which is used in the frame of cosmology: The universe always remains homogeneous and isotropic in the course of its development.

The time-dependent spherical volume belonging to R(t) is expressed through

(4)

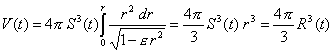
if also here e = 0 is also taken into account. The mass containing contained in this volume is given by

(5)

With r(t) the time-dependent matter density was introduced. This mass remains time constant during the expansion of the universe.

The physical distance between two extragalactic objects picked out arbitrarily and being at the comoving radial coordinate places r₁ and r₂ for a particular but arbitrary time t (e.g. today) is calculated through

(6)

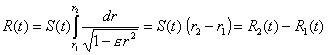
if neither of the two objects is in the coordinate origin (for e = 0). It is now easy now to see that a photon moving independently of the substratum covers the following way between two such galaxies

(7)

if t_E is called the emission time and the absorption time is marked by t_A. For the place of the emission the index Q (light source) was introduced and for the absorption place the index became S (light sink). A simplified expression for the physical quantities that are used here was is introduced behind the last equals sign. It is this light path which has to be taken into account as the apparent distance between two extra galactic systems to calculate the red shift distance relation. This light path is responsible for the weakening of light which finds its expression as apparent magnitude. The light path which was defined with equation (7) is not neither identical with the today's distance (R_SA - R_QA) of between both galaxies and nor equals also not with the distance D with (R_SE - R_QE) between the galaxies at the time of emission of the observed photon.

A maximum possible path is given by S(t_E) = 0 and r_Q = 0, respectively. In this case D_max = R_SA is valid. Since R_QE is generally different from zero in generally case, as a rule the emission place of the photons isn't in the coordinate origin but someplace somewhere between him it and the galaxy, within the photons are observed.

For a particle moving force-free and radial in the matter distribution the conservation law arises from the geodesic equation

(8)

i.e. the product of impulse amount p and world radius S is always constant. From this a redshift z follows for photons with the impulse p = Sw/c corresponding to

(9)

S_A is the value of the world radius at the time t_A of the absorption (index A) of the light particle in the measuring device and S_E is the size of the world radius at the time t_E of the emission (index E) of the photon.

It is the aim of the following considerations to calculate a relation between the redshift z and the apparent distance D. After this D will be exchanged using the apparent magnitude m.

Since a free photon always moves with the constant light velocity c through the Euclidean space (the matter distribution of the universe), the path covered by it during the time between its emission and absorption is given by

(10)

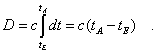
For the description of the movement of the galaxy within the observer stays the Friedmann differential equation

(11)

is used, which is given when solving Einstein's equations with the help of the RWM. This equation describes the time development of the scale parameter and all physical distances in the universe, respectively. For the confirmation of the last-named statement dS/dt is replaced by dR/dt and S by R in accordance with the equations (2) and (3):

(12)

For the mass M which remains constant during the cosmic expansion equation (5) is valid. Therefore the Friedmann equation is converted to

(13)

The integration Integration between in thesuitable boundaries limits yields thereupon

(14)

R_SA was selected as the upper bound of the path integral since the photon and the observer meet at this place at the time t_A. It is noticed to be noted here that R in equation (13) describes the surface of a (Friedmann-) sphere because of using the mass-conservation law (5) during the derivation of this equation. This sphere includes the whole mass M completely. Therefore the observer considered here is on the surface of this matter sphere.

On equating the time intervals of the equations (10) and (14) we get for the way which is covered by the photon

(15)

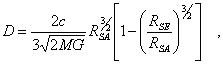
where the unknown physical location R_SE of the observers galaxy at time of the photons emission is still to be eliminated. The relations R_SE = S_Er_S and R_SA = S_Ar_S are very useful, since r = r_S for time t_E and t_A (space expansion because of the time development of S):

(16)

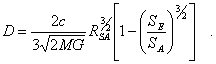
Using equation (9) we get the following intermediate result for the distance-redshift relation we seek for

(17)

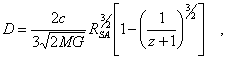
where the factor contains the Schwarzschild radius R_S = 2MG/c² of the mass M which is constant for the observer. According to A. Friedmann the conservation law for this mass is

(18)

Finally this gives the distance-redshift relation

(19)

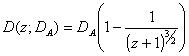
assuming that the limit distance

(19a)

is introduced for the factor, which mainly depends on the current density r_A in the universe only. For this distance z = ¥ is achieved. Besides because of equation (17) it is

(19b)

There is such a limit distance in all steps of the development of the universe, where its size is constantly increasing because of the expansion with time.

The transition to the apparent magnitude m with the help of the well known relationship (A is a constant)

(20)

gives the equation

(21)

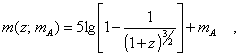
if an apparent magnitude, which corresponds to the present value of D_A, is introduced. This equation only depends on the parameter m_A, which can be fixed by comparing it with a Hubble diagram. Since a Hubble diagram consists of a number of extragalactic objects this comparison gives always a mean value for the apparent magnitude m_A. Therefore the related absolute magnitude M_A has the meaning of an average value too. Thus the average apparent magnitude m_A belongs to a cosmic object with an average absolute magnitude M_A and distance D_A. However, note that the light which was emitted from such an object is infinite red-shifted according to equation (19) and (21), respectively, while arriving at the observer.

The introduced apparent magnitude m_A has the meaning of a limit for present measuring observer and explains the missing of even larger values of m which are caused by the distance. Thus the cut-off effect in the right part of the Hubble diagram is caused by the limited value of the present D_A (see e.g. Djorgovski, Spinrad & Marr 1985, fig. 1 and Yoshii & Takahara 1988, fig. 3 with the explanation: 'The sample galaxies have almost a constant magnitude of V_SM 22-23 mag over the range of z'). Because of the average value nature of the apparent magnitude m_A we will find objects at the right and left hand side of m_A in the Hubble diagram especially for large redshifts.

The curvature of the curve in the Hubble diagram according to equation (21) for large values of the apparent magnitude is an immediate expression of Friedmann's law of expansion (12). It shows that the speed dR/dt at the beginning of the expansion was very large, and that the deceleration of this moving was at that time essentially larger than at later times.

In equation (20) and thus also in the following equations the multiple consideration of the redshift in the form of two (1+z)-factors in the denominator is deliberately neglected (compare with e.g. the derivation of the Hubble law by Sandage 1995). Because of the space expansion during the light travel time the way covered by the photon in the direction of the observer is simply stretched. This process of light attenuation is complete taken into consideration because of the combination of equations (19) and (20). Because of the good agreement of equation (21) with the measurement results both Robertson factors are actually superfluous.

Combining the apparent limit magnitude m_A with the absolute magnitude M, we get for D_A the equation

(22)

where D_A is measured in parsec. Since m_A follows on principle from the Hubble diagram, an independently determined mean absolute magnitude of a star system is enough, to compute D_A. Given D_A, using

(23)

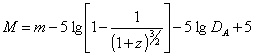
the corresponding absolute magnitude can be calculated for each cosmic system, whose z and m are measured. Inserting the distance module into equation (23) gives directly D_A, assuming z is also known.

Note that the redshift term of equation (23) deviates considerably from those of equation

(xxx)

which can be found in the literature (see e.g. Sandage 1995). This is true especially for large redshifts. Moreover the equation (xxx) does not describe correctly the location of quasars in the Hubble diagram.

Using different spectral ranges (m_pg, U, B, V, R, I, J, H, K, L, b_J, b_F, ...) corresponding different apparent magnitudes (m_pgA, U_A, B_A, V_A, R_A, I_A, J_A, H_A, K_A, L_A, b_JA, b_FA, ...) are expected. This leads to different mean absolute magnitudes.

However not all of the spectral ranges show the theoretical expected slope in the linear part of the Hubble diagram. This fact obviously indicates development effects in the corresponding spectral ranges. Measuring results, which use these spectral ranges, should not be used for evaluation with the help of the here given equations since development effects were not taken into consideration while deriving the equations.

A further important quantity of cosmology is the Hubble parameter. Eliminating z in equation (19) gives

(24)

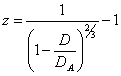
and developing this relation for small ways of light D, yields

(25)

where H_A is the present Hubble parameter.

The interesting thing at equation (25) is the factor 2/3, which is shown by comparing the theory with the astrophysical measuring results. This factor is responsible for the good correspondence between the upper limit of the theoretical "age of the universe" and the age of the spherical cluster of stars.

Note a possible understanding problem relating the common usage of equatios (12) and (5): Using Friedmanns equation (12) and the conservation law of mass (5) means, that the observers galaxy is always situated on the surface of a sphere, which is enclosing the whole mass M, and whose mass density r(t) changes continually with time. This density is constant at any time at all locations as well. Otherwise the conservation law of mass should not be used in the form with r ¹ r(R), since a decomposition of the considered mass into volume and mass density according to equation (5) is only valid for a density, which is independent from the distance R. Because all observers in the universe are equal according to the cosmological principle, each observer is situated on the surface of its own virtual sphere. Since he can as well look in any direction and always will find mass (for instance in form of shining cosmic systems) there, he is surrounded by a multiple of such a virtual spheres which can be theoretical cut out of the universe (and of course partly overlap). The center points (R = 0) are always situated in a distance, which corresponds to the current radius D_A of the mass sphere. If this imagination will be not accepted in this form from the universe which is visible for us, then the Friedmann equation is not useful for the solution of cosmological moving problems in connection with the conservation law of mass, because the Friedmann equation just describes a single mass sphere with a strongly limited surface and radius respectively. Beyond such a surface there is as everybody knows no mass. During the proposed calculation it was shown, that the current radius D_A of this sphere is always the current maximum possible way of light between the light source and the observer. Hereby we just get the limitation of the observable magnitudes of cosmic systems for any time of expansion.

2. COMPARISION WITH ASTROPHYSICAL MEASUREMENTS

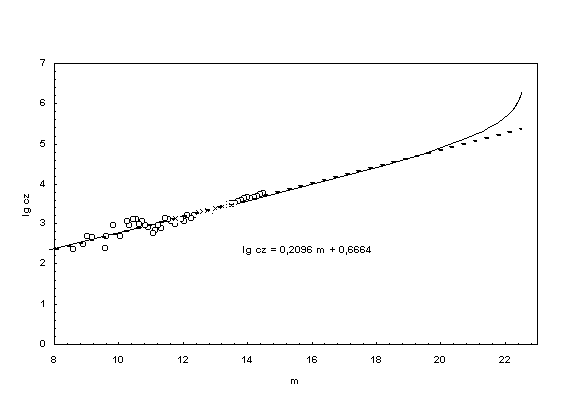
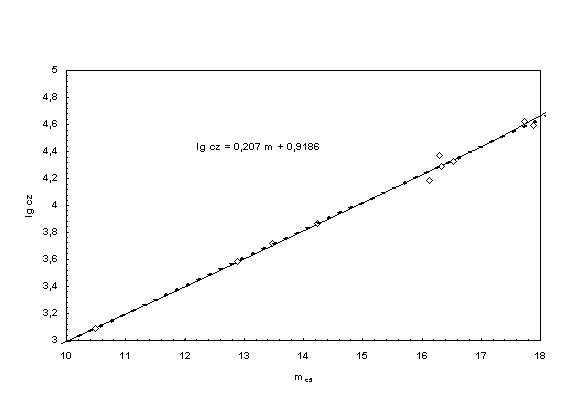
In the literature we can find a multitude of Hubble diagrams. Here the combination by Huchra et al. (1983) is used, to determine the parameter m_A. Since the CfA-catalogue is m-limited, equal m-intervals were formed to evaluate this catalogue of galaxies and the corresponding m- and cz-mean values were determined. The result is shown in Fig. 1, where the mean values are represented by circles. Fitting the theory to the dashed line of best fit through the mean values gives m_A = 22.62. This apparent magnitude has the nature of an average value and using equation (22) an average absolute magnitude M_A can be assigned to assuming that the limit distance D_A is known.

Besides Fig. 1 shows some galaxies of the used catalogue which are represented by crosses and nearly correlated with the best curve. These are the NGC objects 4754, 4608, 4532, 520, 3320, 3888, 1032, 3788, 4224, 3876 as well as 3869. NGC 4754 with m = 11.77 and log cz = 3.138 is the best of these galaxies to obtain agreement with the theory, because it is the apparent brightest compared to the others. For this object the resolution of cepheids is perhaps possible to find the distance module.

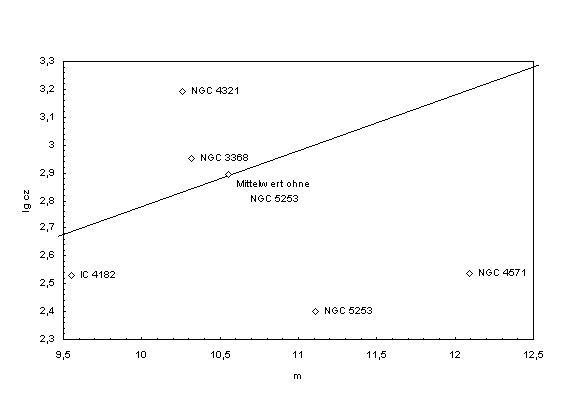
Because there are no distance modules of one of the mentioned objects available, we searched the literature to find well known distance modules. These values were then combined to a Hubble diagram for the cosmic systems M100 = NGC 4321 (Freedman et al. 1994), M96 = NGC 3368 (Tanvir et al. 1995), NGC 5253 (Saha et al. 1995), NGC 4571 (Pierce et al. 1994) and IC 4182 (Sandage et al. 1992), as shown in Fig. 2. Measurements which were not found in this literature were taken from the articles by Huchra et al. (1983), Kraan-Korteweg & Tammann (1979) and Sandage & Tammann (1975). Fortunately the object, which was formed by taking the mean value of the measurements without consideration of NGC 5253, is very close to the theoretical curve fitted with m_A = 22.62. For the mean object we get the absolute magnitude M = -19.91, the apparent magnitude m = 10.56 and the redshift cz = 785.3 km s^-1, which corresponds to log cz = 2.9. Since m_A and M are known in a first approximation, the physical quantities D_A, H_A as well as r_A and the mass M_U can be determined. With the help of equation (22) we get D_A = 3206 Mpc. With this value the Hubble parameter amounts to H_A = 62.34 km Mpc^-1 s^-1. This leads to a Hubble time of t_H = H_A ^-1 = 15.7 x 10⁹ years. Thus there is almost no discrepancy to the assumed age of the oldest spherical star clusters (compare with e.g. Bolte & Hogan 1995). Using equation (19a) we get the current mean density of the visible part of the universe (sphere with radius D_A) r_A = 7.3 x 10^-30 g cm^-3. Thus the expanding sphere has a mass of M_U = 2.96 x 10⁵⁵ g. This mass covers all the components of the metagalaxy which are capable of gravitation: mass from usual particles, radiation and all of the other forms of energy. - If we calculate R_SA with M_U and equation (19b), we get R_SA = D_A, i.e. D_A can be used instead of R_SA in all given formula!

The given values can just be considered as a first approximation, because the calculated mean object lies not exactly on the theoretical curve, and the data are in logarithmic form. Even an insignificant change of one of the input quantities implies relative large shifts of the calculated values. Besides the calculation of the mean value M from only 4 extragalactic objects is critical from a statistical point of view. - Because just the principle of finding the theoretical derived parameter should be explained, no approximations of error limits are given.

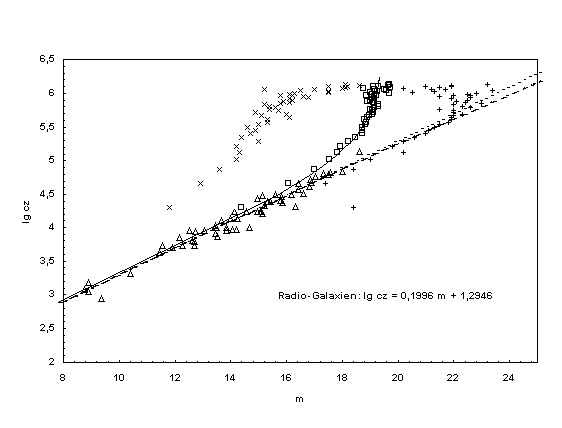
In Fig. 3 the theory is compared with the Hubble diagram of radio galaxies (triangles) according to Sandage (1972). To note the meaning of the new theoretical relations for the quasars this figure shows mean interval values of 13214 quasars (squares) according to Vèron-Cetty et al. (2000). The dotted line is the curve of best fit only through the radio galaxies. With the help of equation (23) the theory was fitted to the quasars, whereby we get a mean absolute magnitude of about M_Q = -23.07 for these cosmic objects. Fitting the theory to the radio galaxies gives an absolute magnitude of M_RG = - 22.8 (Sandage determined M = -22.98 for H₀ = 50 km s^-1 Mpc^-1). The dashed line corresponds to the conventional theoretical derivation of the Hubble law for a deceleration parameter of q₀ = 0.5 assuming that the free available constant is fixed with the help of the galaxies of the CfA catalog [see equation (xxx)]. It is impressive that the new derived theoretical curve goes exactly through the average values of the quasars. Hereby the problem of radiation power of quasars which was so long assumed to be very large can be qualified. On average these objects are not significantly absolute brighter than the radio galaxies. However it shows that the absolute magnitude of quasars varies considerably around the value M_Q. In order to get a better understanding the Hubble diagram shows also the minimum (plus signs) and the maximum (crosses) apparent magnitudes within the intervals. Moreover evaluating this Hubble diagram shows that the redshift could be used as an distance indicator for these quasars, whereas the apparent magnitude is not suitable. Note that equation (xxx) for the Hubble diagram found in the general literature fails at all in the area of large redshifts.

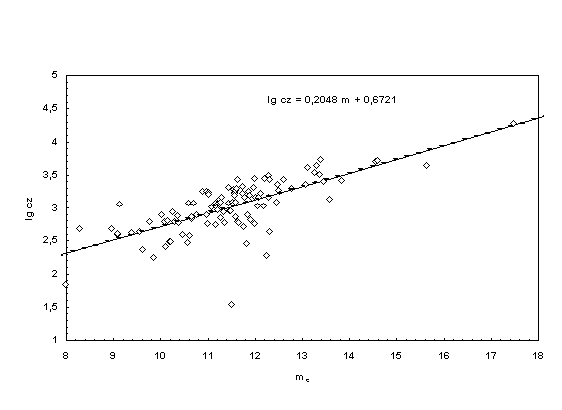
A comparison of the theory with two original Hubble diagrams (Hubble 1936) will be given too. Fig. 4 shows, that the measuring results of field galaxies already listed by Hubble well correspond to the values of modern astrophysics (m_A = 22.3). Fig. 5 gives a mean absolute magnitude of M = -21.6 for the mean values of the brightest cluster galaxies, assuming D_A = 3206 Mpc.

REFERENCES

Bolte, M., Hogan, C.J., 1995, Nature, 376, 399

Djorgovski, S., Spinrad, H., Marr, J., 1985, in New Aspects of Galaxy Photometry, Lecture Notes in Physics 232, 193, ed. Nieto, J. L., (Berlin: Springer Verlag)

Freedman, W. L., et al., 1994, Nature, 371, 757

Hubble, E., 1936, ApJ, 84, 270

Huchra, J., Davis, M., Latham, D., Tonry, J., 1983, ApJS, 52, 89

Kraan-Korteweg, R. C., Tammann, G. A., 1979, Astronomische Nachrichten, 300, 4, 181

Pierce, M. J., Welch, D. L., McClure, R. D., van den Bergh, S., Racine, R., Stetson, P. B., 1994, Nature, 371, 385

Saha, A., Sandage, A., Labhardt, L., Schwengeler, H., Tammann, G. A., Panagia, N., Macchetto, F. D., 1995, ApJ, 438, 8

Sandage, A., 1972, ApJ, 178, 25

Sandage, A., Tammann, G. A., 1975, ApJ, 196, 313

Sandage, A., Saha, A., Tammann, G. A., Panagia, N., Macchetto, D., 1992, ApJ, 401, L7

Sandage, A. R.: in The Deep Universe, Saas-Fee Advanced Course 23, Lecture Notes 1993, edited by B. Binggeli and R. Buser, Springer Verlag, 1995

Tanvir, N. R., Shanks, T., Ferguson, H. C., Robinson, D. R. T., 1995, Nature, 377, 27

Véron-Cetty, M.-P. Véron, P.: A Catalogue of Quasars and Active Nuclei, 9th edition, March 2000, http://www.obs-hp.fr or A&AR (in press)

Yoshii, Y., Takahara, F., 1988, ApJ, 326, 1

FIGURES:

Figure 1.

Hubble diagram according to Huchra et al. (1983). The circles represent the mean values of m-intervals and the crosses show the best galaxies. The dashed straight line is the curve of best fit through the mean interval values of galaxies. The continuous line corresponds to the new theory with m_A = 22.62.

Figure 2.

Hubble diagram according to Freedman et al. (1994), Pierce et al. (1994), Saha et al. (1995), Sandage et al. (1992) and Tanvir et al. (1995) as well as Sandage & Tammann (1975), Kraan-Korteweg & Tammann (1979) and Huchra et al. (1983) to form a mean value object. The continuous line corresponds to the new theory with m_A = 22.62. For further explanations see text.

Figure 3.

Hubble diagram for radio galaxies according to A. Sandage (1972) and quasars according to M.-P. Véron-Cetty (March 2000). The curved continuous line corresponds to the new Hubble relation, which was fitted to the mean interval values of the quasars (squares) with M_Q = -23.07. The dashed line corresponds to the traditional theory. It was fitted to the radio galaxies (triangles). The dotted line is the curve of best fit through the radio galaxies. The crosses on the left hand side of the figure are the maximum apparent magnitude per redshift interval, while the plus signs on the right hand side represent the minimum apparent magnitude of the quasars. On average the quasars are with M_Q = -23.07 only a bit brighter than the radio galaxies, for which was found M_RG = -22.8.

Figure 4.

Redshift-magnitude diagram for field galaxies according to Hubble (1936). The curve of best fit (dashed straight line) gives m_A = 22.3. Here the new theory (continuous line) was k-corrected with a selective term only.

Figure 5.

Redshift-magnitude diagram for the mean values of the brightest cluster galaxies according to Hubble (1936). The curve of best fit (dashed straight line) gives a mean absolute magnitude of M = -21.6 for m_A = 22.62 and D_A = 3206 Mpc. The theory (continuous line) was k-corrected with a selective term only.

Copyright by Steffen Haase, Leipzig, 1998 and 1999

Last update: 03/01/2005
Last correction of spelling mistakes: 11/26/2005