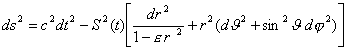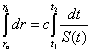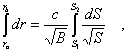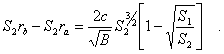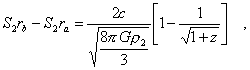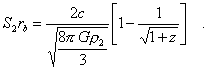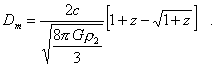Im Folgenden erkläre ich, warum das in der allgemeinen Fachliteratur abgeleitete Hubble-Gesetz [die Gleichung (xxx) in meinem ersten Aufsatz] falsch ist.

1. Vorbetrachtungen

Die Robertson-Walker-Metrik (RWM)

(1)

ergibt sich aus der Forderung nach der Gültigkeit des sogenannten Kosmologischen Prinzips. Sie wird in der theoretischen Kosmologie verwendet, um die bei der zeitlichen Entwicklung des Weltalls erhalten bleibende Homogenität und Isotropie mathematisch richtig beschreiben zu können. Speziell aus der Forderung der Homogenität folgt, dass alle Galaxien im Verlauf der zeitlichen Entwicklung des Universums an ihrem Koordinatenort r¹r(t) verbleiben, d.h. der Koordinatenabstand zwischen zwei beliebig herausgegriffenen Galaxien ändert sich mit der Zeit nicht (die Galaxien ruhen in diesem Koordinatensystem). Für die frei beweglichen Photonen gilt dies nicht: Sie lösen sich zu einem bestimmten Zeitpunkt an einem bestimmten Koordinatenort von einer Galaxie, um dann später an einem ganz anderen Koordinatenort absorbiert zu werden. Zwischen beiden Zeitpunkten verändert sich außerdem der zeitabhängige Skalenparameter S(t).

Wir führen hier für den Koordinatenort der das Licht emittierenden Galaxie die Bezeichnung r_a ein und nennen den Koordinatenort der Galaxie, in der sich der Beobachter aufhält, r_b. Im hier betrachteten euklidischen Raum (e=0) markieren beide Größen den Koordinatenabstand vom Koordinatenursprung. Der zeitlich konstant bleibende Koordinatenabstand zwischen beiden Galaxien berechnet sich demnach zu r_b-r_a, wenn wir annehmen, dass die Galaxie des Beobachters vom Koordinatenursprung weiter entfernt ist, als die das Licht emittierende Galaxie. Das Licht soll sich also innerhalb der kugelförmig gedachten Massenkugel, die als einfaches Modell für das Universum dient, von innen nach außen bewegen (in der RWM lässt es sich ganz einfach einrichten, dass alle Richtungen von radialer Art sind).

Wir wissen, dass im Verlauf der kosmischen Entwicklung sämtliche Abstände über den zeitabhängigen Skalenparameter S(t) gemäß der Friedmann-Gleichung

(2)

gestreckt werden (Expansion des Universums). Diese Gleichung ergibt sich, wenn die Einsteinschen Gleichungen mit Hilfe der RWM gelöst werden. Für das Produkt aus der Materiedichte r und der dritten Potenz des Skalenparameters gilt dann außerdem der Erhaltungssatz

(3)

d.h. A ist eine Konstante mit der Dimension einer Masse, die im wesentlichen der „Gesamt“-Masse des Universums entspricht. Wegen Gleichung (3) kann auch geschrieben werden

(4)

wobei die r_i die Dichten vom Universum und die S_i die Skalenparameter zu zwei verschiedenen Zeitpunkten (i=1,2) bezeichnen. Für die Friedmann-Gleichung folgt mit (3)

(5)

Mit B wurde eine neue Konstante eingeführt. Das Verwenden des Massenerhaltungssatzes (3) bedeutet zugleich, dass sich die für die Expansion verantwortliche Masse des Universums immer innerhalb einer Kugel mit dem gerade aktuellen „Radius“ S befindet. Dies gilt für alle Zeitpunkte.

Für eine im Koordinatensystem der RWM ruhende Galaxie wird der tatsächliche (physikalische) Abstand vom Koordinatenursprung über

(6)

berechnet, d.h. r selbst hängt nicht von der Zeit ab. Der tatsächliche Abstand der das Licht emittierenden Galaxie vom Koordinatenursprung zu einem Zeitpunkt t₁ ist demzufolge

(7)

während für den Abstand der Galaxie, in der sich der Beobachter befindet, zum gleichen Zeitpunkt

(8)

gilt. Wir haben für die Orte der Galaxien die Indizes a bzw. b gewählt (statt 1 bzw. 2), damit es keine Verwechslungen mit den Indizes der Zeitpunkte t₁ bzw. t₂ gibt. Der tatsächliche Abstand zwischen beiden Galaxien zum Zeitpunkt t₁ ist daher

(9)

Für den Abstand zwischen beiden kosmischen Objekten zu einem anderen Zeitpunkt t₂>t₁ gilt dann

(10)

Beide bisher genannten Abstände sind aber für die Berechnung kosmologisch relevanter Beziehungen wertlos, da die emittierten Photonen einen Weg zum Beobachter zurücklegen, der über

(11)

zu berechnen ist. Um das einzusehen, denke man sich ein Photon, dass sich zum Zeitpunkt t₁<t₂ von der emittierenden Galaxie am Koordinatenort r_a löst, wobei der Skalenparameter zu dieser Zeit den Wert S₁ hat. Nachdem sich das Photon kräftefrei durch das Universum bewegt hat, trifft es beim Beobachter innerhalb einer anderen Galaxie am Koordinatenort r_b zum Zeitpunkt t₂ ein, wobei der Skalenparameter zu dieser Zeit den Wert S₂ hat. Das Photon legt also weder den durch die Gleichung (9) noch den durch Gleichung (10) beschriebenen Weg zurück. Der tatsächlich zurückgelegte Lichtweg ist immer größer als jede einzelne dieser beiden Strecken. Entsprechend verändert sich auch die Intensität der Photonen. Das gilt es bei der Ableitung des Hubble-Gesetzes zu beachten.

Diese Anmerkungen mögen als Vorbetrachtung für die nun folgende Ableitung des Helligkeitsabstandes gemäß der allgemeinen Fachliteratur ausreichend sein.

2. Ableitung des Helligkeitsabstandes

Wir wollen nun schauen, wie der von der Rotverschiebung z abhängige Helligkeitsabstand (entspricht dem Photonenweg) formelmäßig aussieht, wenn das in der Literatur übliche Intergral

(12)

verwendet wird. Dieses Integral ergibt sich für e=0, wenn in der RWM (1) das Linienelement gleich null gesetzt wird. Gemäß der Ansicht der Literatur wird durch Gleichung (12) die kräftefreie Bewegung von Photonen im Universum beschrieben, die sich auf den Weg vom Koordinatenort r_a zum Koordinatenort r_b begeben. Während der Reisezeit der Photonen verändert sich der Skalenparameter von S(t₁)=S₁ auf S(t₂)=S₂. Wird das Zeitdifferential mit Hilfe der Friedmann-Gleichung (5) ersetzt, folgt aus Gleichung (12)

(13)

oder nach der Ausführung des Integrals

(14)

Hier multiplizieren wir beide Seiten mit S₂ und ziehen gleichzeitig die Wurzel von S₂ aus den eckigen Klammern heraus:

(15)

Auf der linken Seite der Gleichung (15) steht noch nicht der tatsächlich vom Photon zurückgelegte Weg, sondern der heutige Abstand der beiden beteiligten Galaxien.

Wir führen nun die Rotverschiebung ein. Hierzu erinnern wir uns an den einfachen Zusammenhang zwischen den Skalenparametern zu zwei verschiedenen Zeitpunkten und der Rotverschiebung z:

(16a, b, c)

Wird Gleichung (16b) in die Gleichung (15) eingesetzt, ergibt sich

(17)

Als nächstes müssen alle unbekannten Variablen aus der Gleichung (17) beseitigt werden. Zuerst verwenden wir den Erhaltungssatz (4), um S₂ auf der rechten Seite von Gleichung (17) zu eliminieren. Das Ergebnis ist

(18)

worin r₂ die heutige Massendichte vom Universum beschreibt.

In den Lehrbüchern wird in der Regel fälschlicherweise jede beobachtete Galaxie in den Koordinatenursprung versetzt. Dies entspricht dem Ansatz r_a=0 in Gleichung (18)

(19)

Dieser heutige Abstand der Beobachter-Galaxie S₂r_b vom Koordinatenursprung wird anschließend in die Beziehung

(20)

für den hierdurch definierten Helligkeitsabstand D_m eingesetzt, mit dem Ergebnis

(21)

In den Gleichungen (20) und (21) steht der Index m für das Symbol m der scheinbaren Helligkeit.

Der Faktor (1+z) von Gleichung (20) wird in den Lehrbüchern extra eingeführt, um die durch die Expansion des Universums verursachte Vergrößerung der von der Strahlung am Ort des Beobachters durchdrungenen Fläche zu berücksichtigen, auf die sich die abgestrahlte Energie zum Zeitpunkt t₂ verteilen muss. Der Vergleich von Gleichung (21) mit den Messwerten der Astronomie zeigt aber, dass diese Gleichung trotz des Korrekturfaktors (1+z) nicht die richtige sein kann. Die Einführung eines solchen Faktors ist sofort überflüssig, wenn zur Ableitung des Hubble-Gesetzes die richtige Lichtwegbeziehung (11) zwischen zwei Galaxien benutzt wird und nicht die falsche Gleichung (19).

Die Ursache für die Expansion des Universums ist die in ihm enthaltene Masse bzw. die damit verbundene Massendichte. Sie sorgt dafür, dass sich der Skalenparameter mit der Zeit ändert. Um diese Aussage zu überprüfen, setze man die Materiedichte in der Friedmann-Gleichung einfach gleich null. Ein jeder Kosmologe muss sich nun fragen, wo genau diese Masse im Universum lokalisiert ist. Er kann hierfür einen Anhaltspunkt gewinnen, wenn er sich die passenden Gedanken aus der klassischen Newtonschen Kosmologie leiht. Dort hat er sich eine Massenkugel vorzustellen, deren Radius mit der Zeit wächst. Dies bedeutet, dass sich die in Frage kommende Masse vollständig innerhalb dieser Kugel befindet, und sie dort nach dem Kosmologisches Prinzip gleichmäßig verteilt ist und mit dem Fluss der Zeit auch bleibt. In der relativistischen Kosmologie übernimmt das zeitlich veränderliche Produkt aus Skalenparameter und Koordinatenabstand R(t)=S(t)r die Rolle des tatsächlichen Radius der Massenkugel, und es gilt auch hier, dass sich die gesamte in Betracht zu ziehende Masse innerhalb dieser Kugel befindet. In der Literatur wird jede einzelne beobachtete Galaxie in einen „eigenen“ Koordinatenursprung versetzt (es gibt hier so viele Koordinatenursprünge, wie Galaxien gezählt werden können!), egal in welcher Entfernung vom Beobachter sie auch ist. Da sich wegen der Verwendung des Massenerhaltungssatzes bei der Integration der Friedmann-Gleichung die gesamte Masse immer innerhalb einer Kugel mit dem Radius S₂r_b befinden muss, ergibt sich durch das Nullsetzen von r_a ein Widerspruch, der zum falschen Helligkeitsabstand führt [trotz der künstlichen „Intensitätskorrektur“ mit einem Faktor (1+z)].

Die gleichzeitige Verwendung des Massenerhaltungssatzes (3) beim Integrieren der Gleichung (12) und des Nullsetzens von r_a ist der wesentliche Fehler, der sich in die kosmologische Fachliteratur bereits vor sehr vielen Jahren eingeschlichen hat, und der dort seit Jahrzehnten immer wieder reproduziert wird. Hierdurch kann das Hubble-Gesetz aus den Lehrbüchern (und der sonstigen Literatur) nicht mit den Messergebnissen der Astronomie zur Deckung gebracht werden.

Wiederholung der Fehlerbegründung mit anderen Worten:

Die Gleichung (3) besagt, dass sich die gesamte wirksame Masse M innerhalb einer Kugel mit dem „Radius“ S(t) befindet. Dann gilt aber ebenfalls, dass sich diese Masse auch innerhalb einer Kugel mit dem physikalischen (tatsächlichen) Radius R(t)=S(t)r befinden muss. Da aber in der Literatur (wegen r_a=0) dieser Radius R(t) stets als Abstand zwischen einer beliebigen beobachteten Galaxie und dem Beobachter verwendet wird, und dieser Abstand für (fast) alle beobachteten Galaxien verschieden ist, ergibt sich dort, dass sich die in Betracht zu ziehende Masse M mal in einer kleineren und mal in einer größeren Kugel befinden müsste, je nach dem, wie weit weg die gerade beobachtete Galaxie ist. Dies ist mit Sicherheit falsch!

Copyright:

Die hier veröffentlichten Texte unterstehen dem deutschen und internationalen Urheberrecht, d.h. Veröffentlichungen, Übersetzungen, Übertragungen auf andere Medien etc. - auch von Teilen - sind nur nach vorheriger Genehmigung des Autors gestattet.

Copyright by Steffen Haase, Leipzig (2002)

Letzte inhaltliche Änderung: 07.04.2002

Letzte Schreibfehlerkorrektur: 07.04.2002