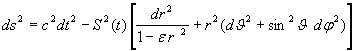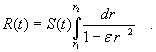Wie ich das Universum sehe [1]
Neulich
habe ich einem Laien den kosmologischen Teil meiner Weltanschauung erklärt.
Lesen
Sie hier, was genau ich ihm vermittelt habe.
Es
liegt nahe, anzunehmen, dass das Universum räumlich unendlich groß ist. Obwohl
die Mathematik mit unendlichen Größen einigermaßen gut umgehen kann,
beschränken wir uns im Folgenden auf einen räumlichen Ausschnitt vom
unendlichen Universum, schon allein deshalb, um das Modell auch etwas
anschaulich darstellen zu können.
Dieser
Anschaulichkeit soll der zweidimensionale Ausschnitt aus dem Universum dienen,
der durch die Projektion des Raumes auf die Ebene eines Stückes Papier gewonnen
werden kann, wie es die Abb. 1 zeigt:
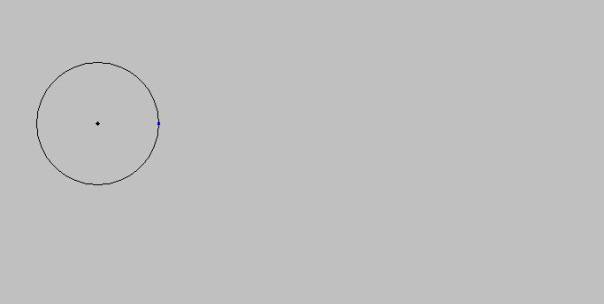
Abb.
1
Ein
weißes Blatt Papier würde einem leeren Universum entsprechen. Weil unser
Universum mit Sicherheit Materie aller Art enthält, wird es in Abb. 1 durch
eine einheitlich graue Fläche dargestellt, die eine - in großen Maßstäben
betrachtet - gleichmäßig verteilte Materiedichte repräsentiert. Das bedeutet
zugleich, dass zu einem beliebig herausgegriffenen Zeitpunkt im Schnitt
nirgends Abweichungen von einer angenommenen
Mittelwertdichte existieren. Die Materiedichte ist demnach nicht vom Ort
der Beobachtung (der Messung) abhängig. [2]
Diese
Annahmen entsprechen der Verwendung des Kosmologischen Prinzips: Das Universum
ist zu allen Zeitpunkten homogen und
isotrop.
Für
die mathematische Beschreibung des uns sichtbaren Universums ist die Verwendung
einer Kugel die geometrisch einfachste Möglichkeit. Durch die von uns verwendete
zweidimensionale Projektion wird eine Kugel zu einem Kreis auf unserem Blatt
Papier [3].
Würden wir das gesamte Universum betrachten wollen, würde die zugehörige Kugel
nicht auf das Blatt Papier passen und beim Rechnen würden wir auch einige
Probleme mit unendlichen Größen bekommen. Aus diesem Grund findet sich in der
Abb. 1 eine Kugel von passender Größe, wobei der Ort der Kugel auf dem Blatt
und deren Größe beliebig gewählt worden sind.
Gewiss
ist es nützlich, wenn sich der Betrachter der Abb. 1 vorstellt, dass er es mit
einem in die Ebene projizierten räumlichen Auszug vom Universum mit den
„Kantenlängen“ von etwa 10.000 * 5.000 (Mpc)2 zu tun hat (1 Mpc =3,086 * 1024 cm).
Als nächstes können wir den Ort eines beliebigen Beobachters festlegen. Hierzu existieren sehr viele Möglichkeiten: Der Beobachter könnte sich im Zentrum der Kugel aufhalten, auf deren Oberfläche oder auch irgendwo sonst innerhalb der Kugel. Wir entschließen uns, den Beobachter, der sich wie wir Erdenbürger gewiss auch auf einem Planeten in der Nähe eines Sternes innerhalb einer Galaxie aufhält, auf der Oberfläche der Kugel anzusiedeln. Weiter unten wird sich noch ein Hinweis darauf ergeben, wo sich der Beobachter tatsächlich befindet.
Nehmen
wir nun an, der Beobachter befinde sich rechts (im „Osten“) vom
Kugelmittelpunkt auf der Kugeloberfläche (blauer Punkt in Abb. 1). Von hier aus
kann er in die Kugel hineinschauen, speziell auch in Richtung des
Kugelmittelpunktes (Blick nach „Westen“). Immer wird er Materie beobachten [4].
Schaut der Beobachter entgegen der Kugelmittelpunktrichtung, d.h. nach „Osten“,
wird er ebenfalls Materie wahrnehmen, die sich allerdings nicht innerhalb der
bisher betrachteten Kugel befindet. Um auch diese Materie zu beschreiben,
ergänzen wir einfach eine weitere gleichgroße Kugel, wie es die Abb. 2 zeigt:
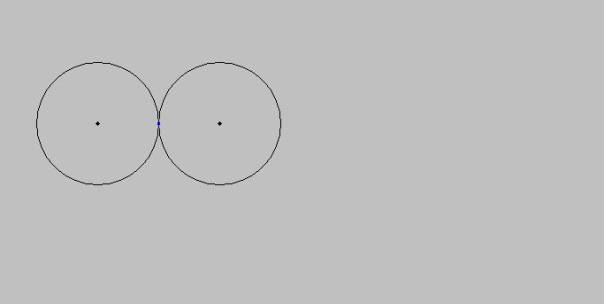
Abb.
2
Anmerkenswert
zu Abb. 2 ist, dass sich die beiden Kugeln nicht überlappen. Ihr Materieinhalt
ist voneinander getrennt.
Mit
den Blickrichtungen nach „Norden“ bzw. nach „Süden“ verfahren wir nun wie mit den
Blicken nach „Osten“ bzw. „Westen“. Hierdurch bekommen wir die Abb. 3:
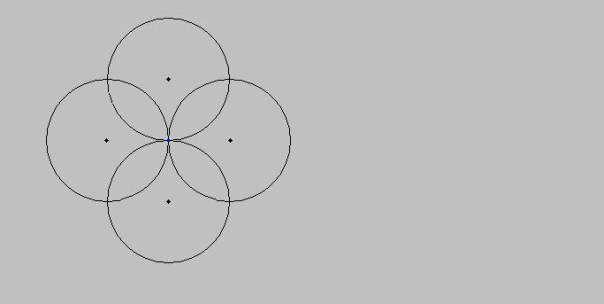
Abb. 3
In Abb. 3 ist nun zu erkennen, dass sich die theoretisch aus dem Universum herausschneidbaren Materiekugeln teilweise überlappen, dass sie Anteile ihrer Materie mit anderen Kugeln gemeinsam haben.
Weitere
Kugeln bekommen wir, wenn der Beobachter z.B. aus dem Blatt Papier „heraus“
schaut (in Richtung des Lesers dieser Zeilen) bzw. in das Blatt „hinein“
schaut. [5]
Diese Kugeln können wir uns ganz einfach vorstellen, obwohl sie auf der
Zeichnungsebene nicht so recht darstellbar sind, auch nicht als Kreise.
Außerdem
sind unendlich viele Beobachter im Universum vorstellbar. Für sie alle ergibt
sich ein Kugelgebilde, wie wir es oben skizziert haben. Die nächste Abbildung
zeigt nur drei beispielsweise mögliche Beobachterstandorte:
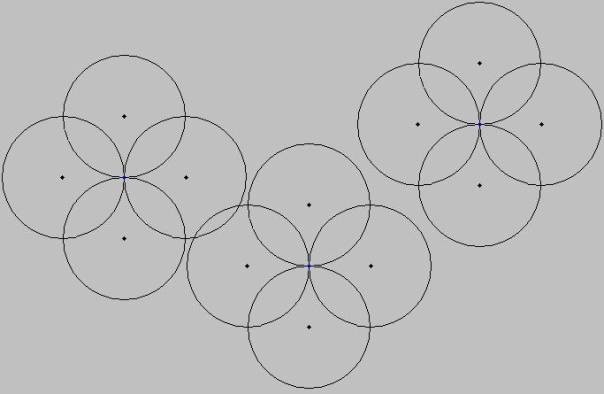
Abb.4
Das Besondere an dieser Abbildung ist, dass sich die zu den einzelnen Beobachtern gehörenden Kugelgebilde im allgemeinen überlappen können, je nach Nähe der Beobachter zueinander. Wir haben das nur an einer Stelle im Bild realisiert und dabei keine besonders große Überlappungstiefe gezeichnet, um die Abbildung nicht zu kompliziert werden zu lassen.
Weil
für jeden möglichen Beobachter unendlich viele Blickrichtungen denkbar sind,
ergeben sich unendlich viele solcher Kugeln je Beobachter, die sich natürlich
meistens überlappen. Die Abb. 5 zeigt z.B. 8 derartige Kugeln: [6]

Abb.
5
Da
alle denkbaren Kugeln identisch sind (Größe und Materieinhalt), ist es
ausreichend, nur eine dieser Kugeln theoretisch zu beschreiben. Genau für diese
mathematische Behandlung des Problems ist die Friedmann-Gleichung bestens
geeignet, die aus den Einsteinschen Feldgleichungen der Allgemeinen
Relativitätstheorie folgt, wenn diese mithilfe der Robertson-Walker-Metrik gelöst
wird. Aus diesem Grund ist es sinnvoll diese Kugeln Friedmann-Kugeln zu nennen.
Die
Friedmann-Gleichung beschreibt eine Friedmann-Kugel als sichtbaren Teil des
Universums, deren Größe sich mit der Zeit verändert. Aktuelle Messwerte deuten
auf eine Expansion dieser Kugel hin.
Wenn
wir annehmen, dass der Radius dieser Kugel heute gerade so groß ist wie der
Weg, der von einem Photon seit Beginn des Expansion zurückgelegt werden konnte,
kann ein Beobachter maximal bis zum Mittelpunkt einer jeden ihn umgebenden
Friedmann-Kugel schauen. Diese erklärt nun die im Bild eingezeichnete innere
Kugel, in deren Mittelpunkt sich der Beobachter befindet: Er kann unter diesen
Umständen keine Kenntnis von Ereignissen bekommen, die außerhalb der Oberfläche
dieser Kugel stattfinden (eigentlich: stattfanden, denn er blickt stets in die
Vergangenheit). Diese innere Kugel ist auch wieder so groß wie die anderen
Kugeln [7],
d.h. sie ist ebenfalls eine Friedmann-Kugel. Obwohl also das Universum
unendlich groß ist, kann ein jeder Beobachter nur Messungen innerhalb dieser
Friedmann-Kugel durchführen.
Durch
diese Betrachtungsweise können wir insgesamt nicht sagen, ob sich der
Beobachter nun auf der Oberfläche von mindestens einer [8]
Friedmann-Kugel befindet, oder im Zentrum einer derartigen Materiekugel. Beides
ist richtig! In der Quantentheorie existiert ein ähnlicher „Effekt“: Wir können
nicht sagen, ob ein Photon ein Teilchen oder ein Welle ist, es trifft beides
zu!
Anhang:
A1) Dimensionsbetrachtungen zur Robertson-Walker-Metrik
An
dieser Stelle wollen wir kurz auf die physikalischen Dimensionen der innerhalb der Robertson-Walker-Metrik (RWM)
|
|
(A1) |
verwendeten
Größen eingehen.
Das
Bogenelement ds hat die Dimension einer Länge, d.h. es wird z.B. in cm oder
auch Mpc gemessen. Die linke Seite der RWM hat demnach die Dimension eines
Längenquadrates.
Das
Produkt aus Lichtgeschwindigkeit c und Zeit t (erster Term der RWM auf der
rechten Gleichungsseite) hat ebenfalls die Dimension einer Länge. Hierdurch
passt die Dimension vom Quadrat des Produktes aus beiden Größen zu der vom
Bogenelement.
Die
Krümmungskonstante e ist dimensionslos. Hieraus
folgt, dass die mitbewegte Radialkoordinate r auch dimensionslos sein muss, da
sie im Nenner vom zweiten rechten Term der RWM im Produkt mit e auftritt und dieses Produkt von der
dimensionslosen Eins abgezogen wird. Deshalb ist der Ausdruck
|
|
(A2) |
insgesamt
ebenfalls dimensionslos. Damit die Terme 2 bis 4 der rechten Seite der RWM die
Dimension eines Längenquadrates haben, muss der Skalenfaktor S(t) die Dimension
einer Länge besitzen, d.h. auch er wird z.B. in Mpc gemessen (1 Mpc =3,086 * 1024 cm).
A2) Zur zeitabhängigen Abstandsveränderung gemäß der Friedmann-Gleichung
Der
Skalenparameter S(t) beschreibt die in der Literatur häufig erwähnte sogenannte
„Raumausdehnung“. Diese „Raumausdehnung“ ist zwar mathematisch denkbar, doch
nicht alles was mathematisch möglich ist, kann im Sinne der Physik
interpretiert werden.
S(t)
allein ist nicht identisch mit dem physikalischen Abstand zwischen zwei
kosmischen Objekten, wie z.B. Galaxien. Auch die dimensionslose und zeitlich
konstante mitbewegte Radialkoordinate r beschreibt keine physikalischen
Abstände. Diese Koordinate dient nur der Nummerierung von Objekten (z.B.
Galaxien), die sich auf ihr befinden, wie die folgende einfache Abb. A1 zeigt:

Abb.
A1
Ein
einmal an seinem mitbewegten Koordinatenort r „angeheftetes“
astrophysikalisches Objekt (blaue Markierungen in Abb. A1) verbleibt während
der Zeit der zeitlichen Entwicklung von S(t) stets an diesem Ort, wenn
allgemein mögliche Eigenbewegungen vernachlässigt werden.
Werden
die Objekte „äquidistant“ angeheftet (z.B. unter Verwendung nur der ganzen
Zahlen wie in Abb. A1 oben), ergibt sich, dass die Materiedichte während der
Expansion des Universums homogen und isotrop gehalten werden kann. Dies ist
eine wesentliche Voraussetzung für die theoretische Kosmologie und die damit
verbundene Verwendung der Robertson-Walker-Metrik (RWM).
Erst
das Produkt aus S(t) und r beschreibt den physikalischen Abstand R(t), wie
sogleich für den Fall des flachen euklidischen Raum gezeigt werden soll.
Hierzu
betrachten wir reine radiale Richtungen gemäß der RWM, d.h. die
Winkel-Differentiale dj und dJ verschwinden beide. Hierdurch nimmt die RWM
die Gestalt
|
|
(A3) |
an.
Zu einem festen aber beliebigen Zeitpunkt (dt = 0) ergibt sich für den
Eigenabstand R(t)
|
|
(A4) |
Beschränken
wir uns nun auf den flachen euklidischen Raum, für den e = 0 anzusetzen ist, erhalten wir die
einfache Gleichung
|
|
(A5) |
für
den zeitabhängigen Eigenabstand zwischen zwei kosmischen Objekten, die sich
jeweils an den mitbewegten Koordinatenorten r1 bzw. r2
aufhalten.
Demnach
gilt ganz allgemein R(t) = S(t)r für den sich zeitlich entwickelnden Abstand ,
wenn eines der beiden Objekte in den Koordinatenursprung (r = 0) versetzt wird.
Zur besseren Veranschaulichung sei noch folgende Abb. A2 erläutert:
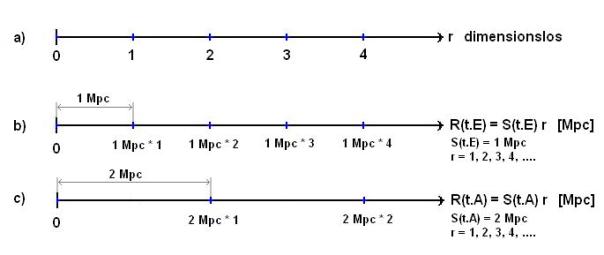
Das
Teilbild a) zeigt wieder die mitbewegte Radialkoordinate. Die angegebenen
Zahlen nummerieren entlang dieser Koordinate „äquidistant“ gelegene kosmische
Objekte.
Für
das Teilbild b) wurde ohne Einschränkung der Allgemeinheit angenommen, dass zum
Zeitpunkt tE der Emission eines später zum Zeitpunkt tA beobachteten d.h. absorbierten Photons der Skalenparameter S(tE)
gerade 1 Mpc betrug (ein einfach zu handhabender Beispielzahlenwert). Hierdurch
haben zum beliebig gewählten Zeitpunkt tE alle mittels r
durchnummerierten und sich auf der Koordinatenachse nebeneinander befindlichen
Objekte gerade den Abstand von 1 Mpc.
Das
Teilbild c) zeigt die Abstände der kosmischen Objekte zum Zeitpunkt tA,
wenn das Photon gerade absorbiert wird. Der Skalenparameter S(tA)
wurde hier zu 2 Mpc gewählt.
Es
ist deutlich zu erkennen, dass alle Objekte nach wie vor an ihrem
Koordinatenort r verweilen, sich der physikalische Abstand zwischen jeweils
zwei Objekten aber verdoppelt hat.
A3)
Zum von Photonen zurückgelegten Weg (Lichtweg)
Wir
nehmen als Beispiel an, dass sich ein Photon zum Zeitpunkt tE am
physikalischen Ort R1(tE) = S(tE)r1
= 1 Mpc * 1 = 1 Mpc [wegen S(tE) = 1 Mpc und r1 = 1] von
der das Licht emittierenden Galaxie (Lichtquelle) löst, um zu einem späteren
Zeitpunkt tA am physikalischen Ort R2(tA) =
S(tA)r2 = 2 Mpc * 2 = 4 Mpc [wegen S(tA) = 2
Mpc und r2 = 2] einer anderen Galaxie (Lichtsenke) absorbiert zu
werden. Die Abb. A3 zeigt den vom Photon zwischen den Zeitpunkten tE
und tA zurückgelegten Weg D:
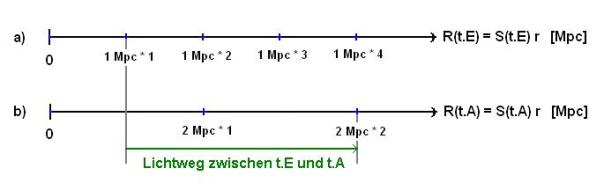
Abb. A3
In
Abb. A3 ist deutlich zu sehen, dass der Lichtweg D = R2(tA)
– R1(tE) = S(tA)r2
– S(tE)r1 größer ist, als der heutige Abstand D(tA)
= R2(tA) – R1(tA) = S(tA)r2
– S(tA)r1 = S(tA)[r2 – r1]
zwischen den beiden willkürlich ausgewählten Galaxien. Auch der Abstand beider
Galaxien zum Zeitpunkt tE ist mit D(tE) = R2(tE)
– R1(tE) = S(tE)r2
– S(tE)r1 = S(tE)[r2 – r1]
kleiner als der heutige Abstand D(tA), weil im Falle einer Expansion
des Universums S(tE) < S(tA) gilt. D(tE)
ist natürlicherweise der kleinste hier betrachtete Abstand, während der
Lichtweg D der größte ist.
Die
Abschwächung der Intensität I des Lichtes nach dem Abstandsquadratgesetz (I µ 1/D2) wird durch den von den
Photonen zurückgelegten Lichtweg D verursacht. Dieser entspricht weder der
heutigen Entfernung zwischen den beiden betrachteten Galaxien noch der
Entfernung zum Zeitpunkt der Lichtemission! Es handelt sich demnach um einen
„scheinbaren“ Abstand.
Copyright:
Die hier veröffentlichten Texte unterstehen dem deutschen und internationalen
Urheberrecht, d.h. Veröffentlichungen, Übersetzungen, Übertragungen auf andere
Medien etc. - auch von Teilen - sind nur nach vorheriger Genehmigung des Autors
gestattet.
Copyright by Steffen Haase, Greifswald (1998) and Leipzig (1999)
Letzte
inhaltliche Änderung: 18.01.2007
Letzte
Schreibfehlerkorrektur: 04.03.2007