Weg-Zeit-Diagramm für Galaxien und Photonen gemäß der Friedmann-Gleichung
Das Folgende Bild dient der
Veranschaulichung der physikalischen Bewegungsabläufe in einem nach der
Friedmann-Gleichung expandierenden Universum für den Fall verschwindender
Raumkrümmung (euklidischer Raum mit e = 0 in
der Robertson-Walker-Metrik). Es zeigt die zeitliche Veränderung des Radius'
der Friedmann-Kugel und die davon unabhängige Bewegung der Photonen von den
beobachteten Galaxien hin zum Beobachter.
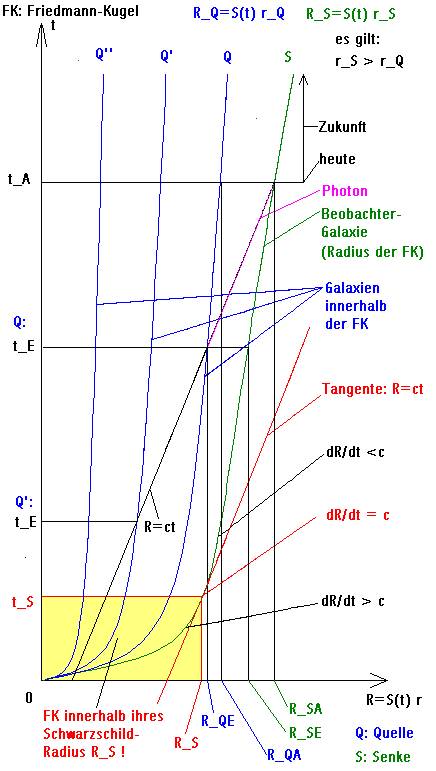
Ein beliebiger Beobachter (grüne Kurve)
befindet sich innerhalb seiner Galaxie ("Beobachter-Galaxie") stets
auf der Oberfläche einer Friedmann-Kugel (FK) mit dem Radius R(t) = S(t)r, die
sich gemäß der Friedmann-Gleichung ungleichförmig ausdehnt und die die gesamte,
in die Gleichung (I,13)
![]()
eingehende, Masse M enthält, die zu
allen Zeitpunkten gleichmäßig in der FK verteilt ist und auch bleibt (für die
mitbewegte Radialkoordinate r gilt immer r = konstant für alle Galaxien).
Egal an welchem Punkt sich der
Beobachter im Universum befindet, er schaut beim Beobachten bzw. Messen immer
in eine FK hinein, wobei es keine Rolle spielt, welche Beobachtungsrichtung er
dabei auswählt (Kosmologisches Prinzip: homogenes und isotropes Universum).
Zum Anfangszeitpunkt t = 0 sind wegen
S(t) = 0 alle Abstände R(t) = S(t)r innerhalb der FK unendlich klein und der
Radius der FK ist ebenfalls Null (Anfangssingularität) [1]. Zu diesem Zeitpunkt beginnt sich das Universum
auszudehnen, wodurch sich der Radius der FK entsprechend der
Friedmann-Gleichung vergrößert und hierdurch auch sämtliche Abstände innerhalb
der FK wachsen.
In der Frühzeit der Expansionsbewegung
ist die Änderungsgeschwindigkeit dR/dt vom FK-Radius sogar größer als die
Lichtgeschwindigkeit c (gelb markierter Bereich im Bild). Sie erreicht die
Lichtgeschwindigkeit zur Schwarzschild-Zeit tS, wenn der Radius
gerade dem Schwarzschild-Radius RS der in die Friedmann-Gleichung
eingehenden Masse M entspricht (Ort der roten Tangente R = ct an der grüne
Kurve). Ab diesem Zeitpunkt strebt die Radiusänderungsgeschwindigkeit mit
Unterlichtgeschwindigkeit dem Wert Null entgegen, der aber erst in unendlich
ferner Zeit erreicht wird.
Alle Ereignisse im Universum werden dem
Beobachter über Photonen vermittelt, die sich z.B. entlang der schrägen
schwarzen Geraden R = ct durch die FK bewegen (für Photonen ändert sich der
Koordinatenabstand r während ihrer Reise durch das Universum). Hierdurch sieht
er das Licht von Galaxien, die es zu unterschiedlichen Zeitpunkten tE
emittiert haben, als auch die zugehörigen Skalenparameter S(tE) = SE
unterschiedlich groß waren. Die Quotienten aus dem heutigen Skalenparameterwert
S(tA) = SA und den jeweiligen Werten zu den
unterschiedlichen Emissionszeitpunkten S(tE) sind gemäß Gleichung
(I,9)
![]()
für die messbaren Rotverschiebungen
verantwortlich.
Im Bild sind beispielhaft drei innerhalb
der FK befindliche Galaxien Q'', Q' und Q (Lichtquellen) eingezeichnet, für die drei verschiedene SE
gelten, um das deutlich werden zu lassen. Außerdem sind für die Lichtquelle Q einige Abstandsbezeichnungen
angegeben, die sich auch im ersten Aufsatz finden. Speziell ist für dieses
Beispiel der tatsächliche Lichtweg D = RSA – RQE zu
erkennen, der indirekt in die Berechnung des Rotverschiebungsabstandes als
"scheinbare" Entfernung eingeht. Der Begriff "scheinbar"
wird hier verwendet, weil dieser Abstand nicht dem heutigen Abstand zwischen
Lichtquelle Q und Lichtsenke S entspricht. Dieser berechnet sich über RSA
– RQA. Die "scheinbare" Entfernung D, d.h. der vom Photon
tatsächlich zurückgelegte Weg, ist für die Schwächung der Intensität des
Lichtstrahles während der Lichtlaufzeit tA - tE
verantwortlich und korrespondiert deshalb mit der scheinbaren Helligkeit m.
Sicherlich hilft es dem Betrachter des
Bildes, wenn er sich die Beobachtergalaxie beim dimensionslosen
Koordinatenabstand r = 1 vorstellt. Dann wären die im Bild außerdem noch
eingezeichneten Galaxien Q'', Q' und Q etwa bei r'' = 0,25, r' = 0,5
und r = 0,75 angesiedelt. Das gilt für den Zeitpunkt tA (heute)
genauso, wie für den Zeitpunkt tS (Schwarzschild-Zeit), als die FK
gerade so groß war, wie es ihr Schwarzschild-Radius RS = 2MG/c2
ausdrückt. Insofern ist die Zeichnung einigermaßen maßstabsgetreu. Das Gebiet,
das den Schwarzschild-Zustand vom Universum (alle FK haben dann gerade den
Radius R = RS, gelbes Rechteck) beschreibt, ist im Bild übergroß
dargestellt, um es besser wahrnehmen zu können.
Alle Galaxien, deren Bewegungskurve die
schwarze Gerade R = ct schneidet, sind heute (t = tA) schon
beobachtbar. Die Abbildung zeigt sehr deutlich, dass das für die Galaxie Q''
nicht zutrifft. Diese Galaxie wird erst
in der Zukunft sichtbar. Das ist unmittelbar zu erkennen, wenn die Gerade etwas
nach links parallelverschoben wird, bis sie die Bewegungskurve der Galaxie Q''
schneidet. Hierbei verschiebt sich auch der Schnittpunkt der Geraden mit der
Beobachter-Galaxie in die Zukunft. Mit der Zeit werden schließlich alle
Galaxien der FK sichtbar.
Werden aus einleuchtenden physikalischen
Gründen keine Überlichtgeschwindigkeiten dR/dt > c für die Expansion des
Universums zugelassen, beginnt die Expansion erst bei tS bzw. RS,
wobei dann das Weltalter sinnvollerweise auf tS = 0 normiert werden
sollte. In diesem Fall expandiert das Universum zwar auch, aber es hat keinen
Urknall gegeben. Hierzu sind einige Anmerkungen im vierten Aufsatz zu finden.
Copyright:
Die hier veröffentlichten Texte unterstehen dem deutschen und
internationalen Urheberrecht, d.h. Veröffentlichungen, Übersetzungen,
Übertragungen auf andere Medien etc. - auch von Teilen - sind nur nach
vorheriger Genehmigung des Autors gestattet.
Die Rechte von Teilen einiger Abbildungen liegen bei den Verlagen der jeweils
angegebenen Quelle.
Copyright by Steffen Haase,
Greifswald (1998) and Leipzig (1999)
Letzte inhaltliche Änderung: 17.12.2005
Letzte Schreibfehlerkorrektur: 04.03.2007